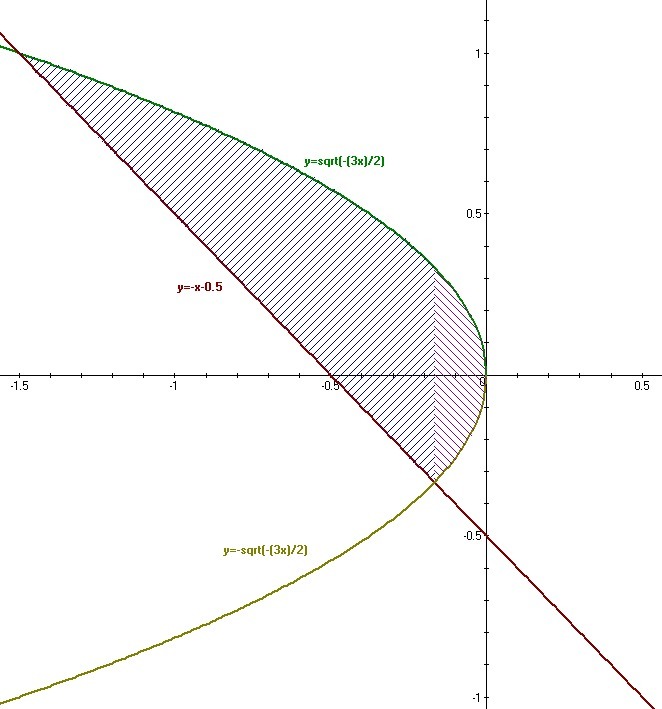
Вычислить площадь плоской фигуры ограниченной заданными кривыми. Сделать чертеж полученной области 2x+3y^2=0, 2x+2y+1=0
Ответы
Ответ дал:
0
Выразим y из обоих выражений:

Теперь нужно найти точки пересечений:

А теперь площади, обращаем внимание, что тут будет сумма площадей.

Теперь нужно найти точки пересечений:
А теперь площади, обращаем внимание, что тут будет сумма площадей.
Приложения:
Вас заинтересует
2 года назад
2 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад