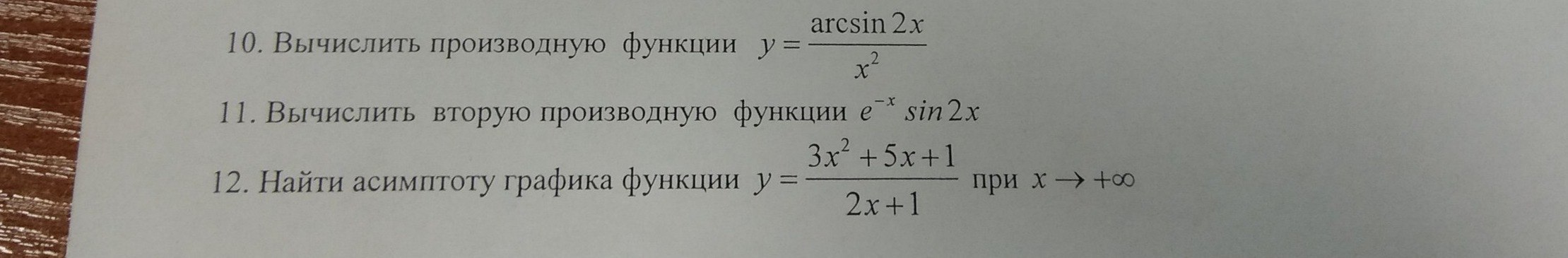Ответы
Ответ дал:
1
10. Воспользуемся формулой производной частного.

11. Здесь пользуемся формулой производной произведения.

Вторая производная:

12. Наклонная асимптота является линейной функцией. В общем виде можно представить как y = kx + b
По определению асимптоты:

Найдем теперь коэффициент b

Получим уравнение наклонной асимптоты:
11. Здесь пользуемся формулой производной произведения.
Вторая производная:
12. Наклонная асимптота является линейной функцией. В общем виде можно представить как y = kx + b
По определению асимптоты:
Найдем теперь коэффициент b
Получим уравнение наклонной асимптоты:
Вас заинтересует
1 год назад
1 год назад
2 года назад
3 года назад
8 лет назад
8 лет назад