Question

Точка О лежит внутри треугольника ABC. Отрезок OP(P э AC) параллелен стороне BC. Треугольник ABC разделили на части. Вычислите длину радиуса окружности,описанной около треугольника AOP, если известно, что AO = 4см, угол ACB = 60градусов

Answer 1

∠APO=∠ACB=60° (соответственные углы при OP||BC)

По теореме синусов, △AOP

АО/sin(APO) =2R

R =4 *2/√3 *1/2 =4√3/3 (см)

Напомним доказательство теоремы синусов.

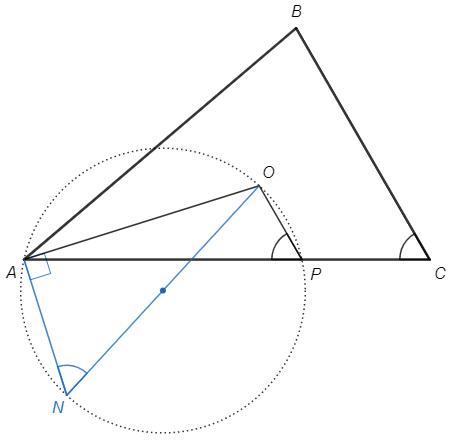
Пусть ON - диаметр описанной окружности треугольника AOP.

∠OAN=90° (вписанный угол, опирающийся на диаметр)

∠ANO=∠APO (вписанные углы, опирающиеся на одну дугу)

sin(ANO) =AO/ON => AO/sin(ANO) =ON =2R