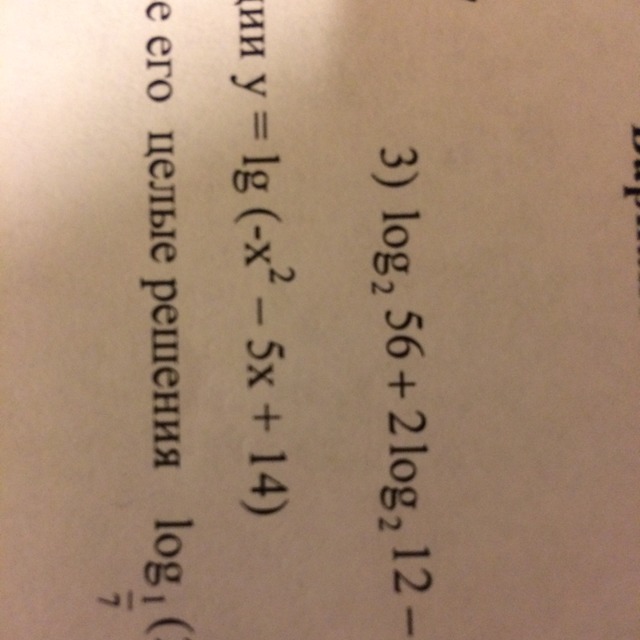Ответы
Ответ дал:
0
По определению логарифма выражение

Имеет смысл только при x > 0, следовательно:
ООФ:

Решаем неравенство:
1) Делим обе части на -1

2) Приравниваем к нулю, чтобы найти корни:

Используем теорему обратную теореме Виета:

Получаем, что

3) Наносим корни на числовую ось и решаем неравенство с помощью метода интервалов:
Получаем:
Промежутки ( - бесконечность ; -7 ) и ( 2 ; + бесконечность ) имеют знак "+"
Промежуток (-7;2) знак "-"
Нас просили найти когда выражение меньше нуля:

Т.о OOФ: х принадлежит (-7;2)
Имеет смысл только при x > 0, следовательно:
ООФ:
Решаем неравенство:
1) Делим обе части на -1
2) Приравниваем к нулю, чтобы найти корни:
Используем теорему обратную теореме Виета:
Получаем, что
3) Наносим корни на числовую ось и решаем неравенство с помощью метода интервалов:
Получаем:
Промежутки ( - бесконечность ; -7 ) и ( 2 ; + бесконечность ) имеют знак "+"
Промежуток (-7;2) знак "-"
Нас просили найти когда выражение меньше нуля:
Т.о OOФ: х принадлежит (-7;2)
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад
10 лет назад