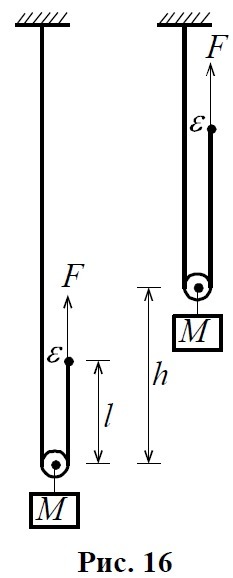
Груз массой M поднимают с помощью подвижного блока массой m и радиуса R (см. рис. 16), прикладывая к правому концу верёвки (точке ε) силу F. Верёвка нерастяжима, масса одного метра длины верёвки μ. Начальная длина части верёвки правее блока l. Блок медленно подняли на высоту h. На сколько при этом увеличилась потенциальная энергия верёвки? Чему равен КПД блока с учётом конечности массы блока и массы верёвки?
Приложения:
Ответы
Ответ дал:
0
пропущенная через блок веревка состоит из двух частей длина которых
х - слева от блока
у - справа от блока
х+у=L
положение центра масс веревки слева -х/2
положение центра масс веревки справа -х+у/2
потенциальная энергия веревки
W=x*μ*g*(-х/2)+y*μ*g*(-х+у/2)=μ*g*(х*(-х/2)+y*(-х+у/2))=
=-μ*g*(х^2+2y*х-у^2))/2=-μ*g*(х^2+2y*х+у^2-2у^2))/2=
=-μ*g*((х+y)^2-2у^2))/2=-μ*g*L^2/2+μ*g*у^2
изменение потенциальной энергии при изменении величины у с l до l+h
-μ*g*L^2/2+μ*g*(l+h)^2 -( -μ*g*L^2/2+μ*g*l^2) =μ*g*(l+h)^2 -μ*g*l^2 =
=μ*g*h*(2l+h) - Это ответ (1)
чтобы потратить груз массой М на высоту h приходится тратить полезную энергию Mgh а также mgh и μ*g*h*(2l+h)
кпд = Mgh / (Mgh + mgh + μ*g*h*(2l+h)) = M / (M + m + μ*(2l+h)) - Это ответ (2)
х - слева от блока
у - справа от блока
х+у=L
положение центра масс веревки слева -х/2
положение центра масс веревки справа -х+у/2
потенциальная энергия веревки
W=x*μ*g*(-х/2)+y*μ*g*(-х+у/2)=μ*g*(х*(-х/2)+y*(-х+у/2))=
=-μ*g*(х^2+2y*х-у^2))/2=-μ*g*(х^2+2y*х+у^2-2у^2))/2=
=-μ*g*((х+y)^2-2у^2))/2=-μ*g*L^2/2+μ*g*у^2
изменение потенциальной энергии при изменении величины у с l до l+h
-μ*g*L^2/2+μ*g*(l+h)^2 -( -μ*g*L^2/2+μ*g*l^2) =μ*g*(l+h)^2 -μ*g*l^2 =
=μ*g*h*(2l+h) - Это ответ (1)
чтобы потратить груз массой М на высоту h приходится тратить полезную энергию Mgh а также mgh и μ*g*h*(2l+h)
кпд = Mgh / (Mgh + mgh + μ*g*h*(2l+h)) = M / (M + m + μ*(2l+h)) - Это ответ (2)
Вас заинтересует
2 года назад
2 года назад
3 года назад
9 лет назад
10 лет назад