Question

В прямоугольном треугольнике АВС катет АС=40 и гипотенуза АВ=41. Найдите sin A,CosA,tgA

Answer 1

 АВ=41 sin A 41+CosA
 CosA=20
 АВ=41-CosA20=21
tgA=46
46-21=25
Ответ 25

Answer 2

Ответ:

sin∠A=9/41

Cos∠A=40/41

tg∠А=9/40

Пошаговое объяснение:

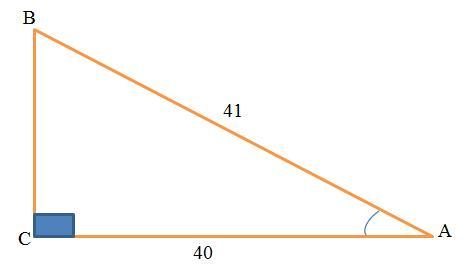
Дано (см. рисунок):

ΔАВС

∠С=90°

катет АС=40

гипотенуза АВ=41

Найти: sin∠A, Cos∠A, tg∠А

Решение.

Треугольник АВС прямоугольный, поэтому применив теорему Пифагора находим катет ВС, то есть из АВ²=АС²+ВС² получим

ВС²=АВ²-АС²=41²-40²=1681-1600=81=9².

Отсюда ВС=9. По определению:

sin∠A=ВС/АВ=9/41

Cos∠A=АС/АВ=40/41

tg∠А=ВС/АС=9/40.

Ответ:

sin∠A=9/41

Cos∠A=40/41

tg∠А=9/40.