Question

СРОЧНО
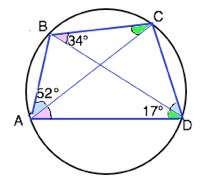
Четырехугольник ABCD вписан в окружность, ∠BAC = 52 градуса, ∠DBC = 34 градуса, ∠ADB = 17 градусов. Найдите углы четырехугольника.

Answer 1

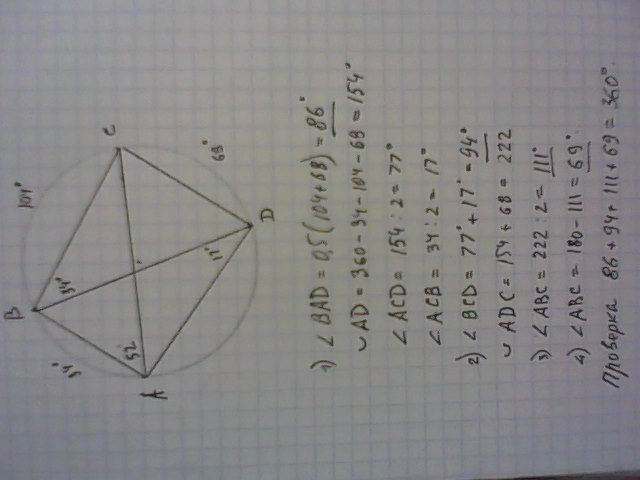
Смотри на фото рисунок и решение

Answer 2

Вписанные углы, опирающиеся на одну дугу, равны.⇒ 

Угол САD = ∠CBD=34°⇒

     угол BAD= ∠BAC+∠CAD=52°+34°=86° 

Четырёхугольник можно вписать в окружность тогда и только тогда, когда сумма его противоположных углов равна 180°⇒

       угол BCD=180°- ∠BAD=180°-86°=94° 

∠BCA = ∠BDA =17° (опираются на одну дугу) ⇒ 

∠ACD=∠BCD-∠BCA=94°-17°=77°

Вписанный угол АВD=∠ACD = 77°  – опираются на одну дугу.  

       угол АВС=<АВD+<CBD=77°+34°=111°

∠СDB=∠BAC=52°⇒

       угол ADC=17°+52°=69°