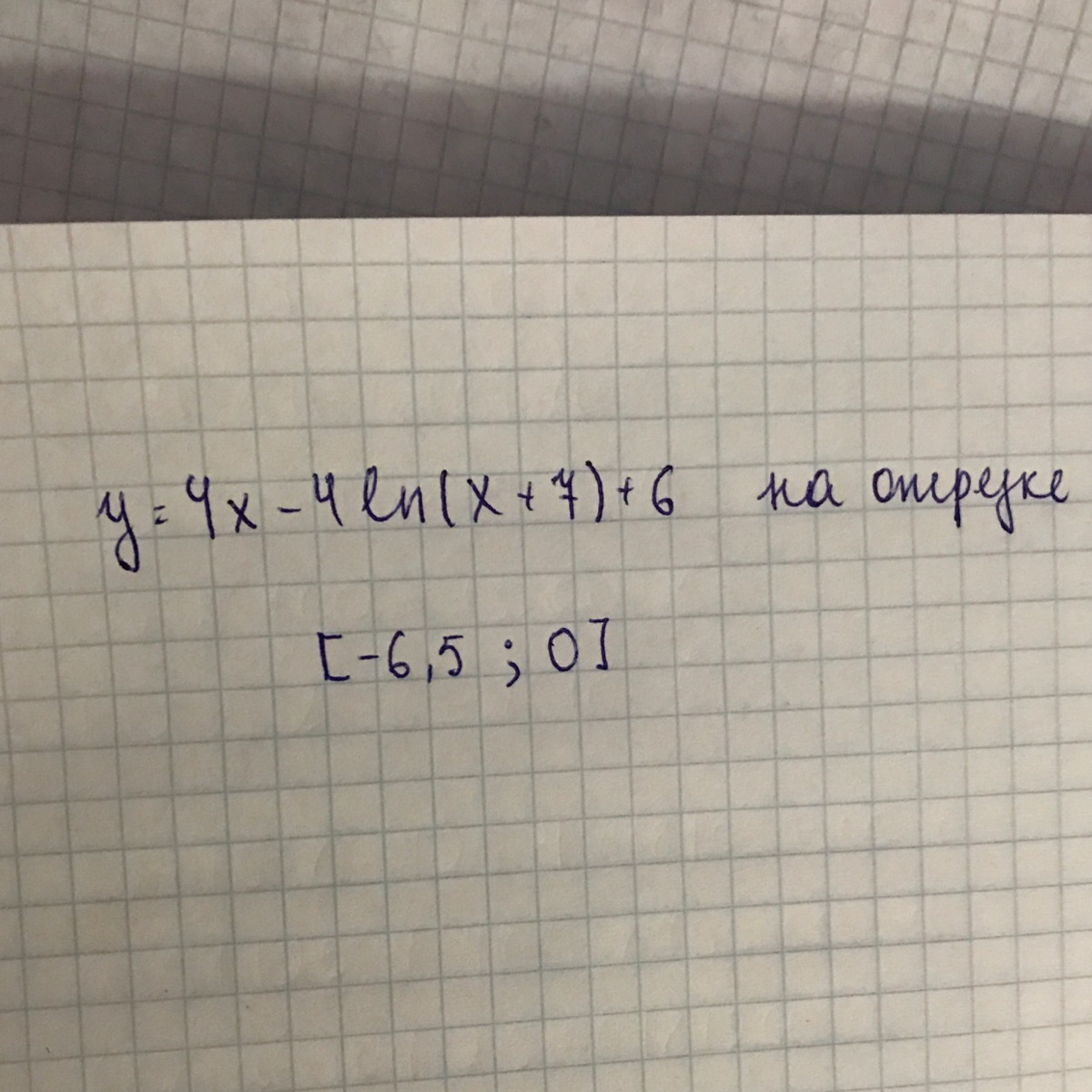Question

Найдите наименьшее значение функции( ДАЮ 30 БАЛЛОВ)

Answer 1

$y=4x-4ln(x+7)+6 ;;;;; mid ;;; [-6,5;0] \ \ y'(x)=4- frac{4}{x+7} \ \ y'(x)=0: \ \ 4- frac{4}{x+7} =0 ;;;; x neq -7 \ \ -frac{4}{x+7}=-4 \ \ 4=(x+7)*4 \ \ x=-6 \ \ +++++(-7)-----[-6]+++++$

Экстремумы функции :

С + на - значит $x_{max}$ , с - на + значит $x_{min}$

Так как -6 входит в промежуток от -6,5 к 0 , значит  $x_{min}=-6$

Подставим $x_{min}$ в y:

$y=4x-4ln(x+7)+6 \ \ y_{min}=4*(-6)-4ln(-6+7)+6 \ \ y_{min}=-24-underbrace{4ln(1) }_{=0}+6 \ \ y_{min}=-24+6 \ \ y_{min}=-18$

Ответ: Наименьшего значение функция на интервале [6,5;0] будет в точке $(-6;-18)$

Answer 2

Помогите ЛЮДИ АУ У МЕНЯ АЛГЕБРА НОМЕР 246 ПЛИЗЩЗЖЖЖЗЗЗЗЗЗЕЦИЛ

Answer 3

Сори если не по теме! -_-