Ответы
Ответ дал:
0
Рассмотрим неопределенный интеграл:
![int frac{xdx}{ sqrt[4]{(15x^2+1)^3}} = frac{1}{30} int frac{d(15x^2+1)}{ sqrt[4] {(15x^2+1)^3}} = frac{1}{30} int (15x^2+1)^{ -frac{3}{4} }d(15x^2+1) =\
= frac{1}{30}(15x^2+1)^{ frac{1}{4}} + C = frac{1}{30} sqrt[4]{15x^2+1}} + C int frac{xdx}{ sqrt[4]{(15x^2+1)^3}} = frac{1}{30} int frac{d(15x^2+1)}{ sqrt[4] {(15x^2+1)^3}} = frac{1}{30} int (15x^2+1)^{ -frac{3}{4} }d(15x^2+1) =\
= frac{1}{30}(15x^2+1)^{ frac{1}{4}} + C = frac{1}{30} sqrt[4]{15x^2+1}} + C](https://tex.z-dn.net/?f=int++frac%7Bxdx%7D%7B+sqrt%5B4%5D%7B%2815x%5E2%2B1%29%5E3%7D%7D+%3D+frac%7B1%7D%7B30%7D+int++frac%7Bd%2815x%5E2%2B1%29%7D%7B+sqrt%5B4%5D+%7B%2815x%5E2%2B1%29%5E3%7D%7D+%3D++frac%7B1%7D%7B30%7D+int+%2815x%5E2%2B1%29%5E%7B+-frac%7B3%7D%7B4%7D+%7Dd%2815x%5E2%2B1%29+%3D%5C%0A%3D+frac%7B1%7D%7B30%7D%2815x%5E2%2B1%29%5E%7B+frac%7B1%7D%7B4%7D%7D+%2B+C+%3D+frac%7B1%7D%7B30%7D+sqrt%5B4%5D%7B15x%5E2%2B1%7D%7D+%2B+C)
Используем пределы интегрирования:
![int limits_{0}^{1} frac{xdx}{ sqrt[4]{(15x^2+1)^3}} = frac{1}{30} sqrt[4]{15x^2+1}} big | _{0}^{1} = frac{1}{30}sqrt[4]{15+1}- frac{1}{30}sqrt[4]{0+1}=\
=frac{1}{30}*2-frac{1}{30} = frac{1}{30}. int limits_{0}^{1} frac{xdx}{ sqrt[4]{(15x^2+1)^3}} = frac{1}{30} sqrt[4]{15x^2+1}} big | _{0}^{1} = frac{1}{30}sqrt[4]{15+1}- frac{1}{30}sqrt[4]{0+1}=\
=frac{1}{30}*2-frac{1}{30} = frac{1}{30}.](https://tex.z-dn.net/?f=int+limits_%7B0%7D%5E%7B1%7D+frac%7Bxdx%7D%7B+sqrt%5B4%5D%7B%2815x%5E2%2B1%29%5E3%7D%7D+%3D+frac%7B1%7D%7B30%7D+sqrt%5B4%5D%7B15x%5E2%2B1%7D%7D+big+%7C+_%7B0%7D%5E%7B1%7D++%3D++frac%7B1%7D%7B30%7Dsqrt%5B4%5D%7B15%2B1%7D-+frac%7B1%7D%7B30%7Dsqrt%5B4%5D%7B0%2B1%7D%3D%5C%0A%3Dfrac%7B1%7D%7B30%7D%2A2-frac%7B1%7D%7B30%7D+%3D+frac%7B1%7D%7B30%7D.)
Используем пределы интегрирования:
Приложения:
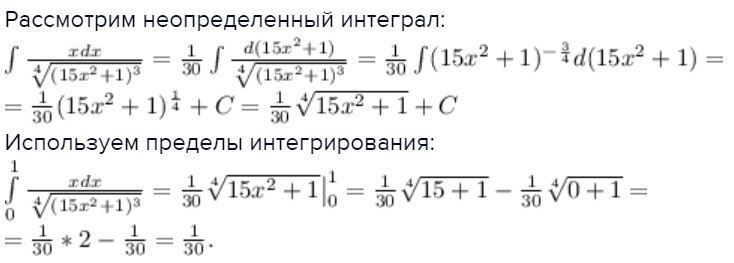
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад