Ответы
Ответ дал:
0
ответ на фото. удачи!
Приложения:
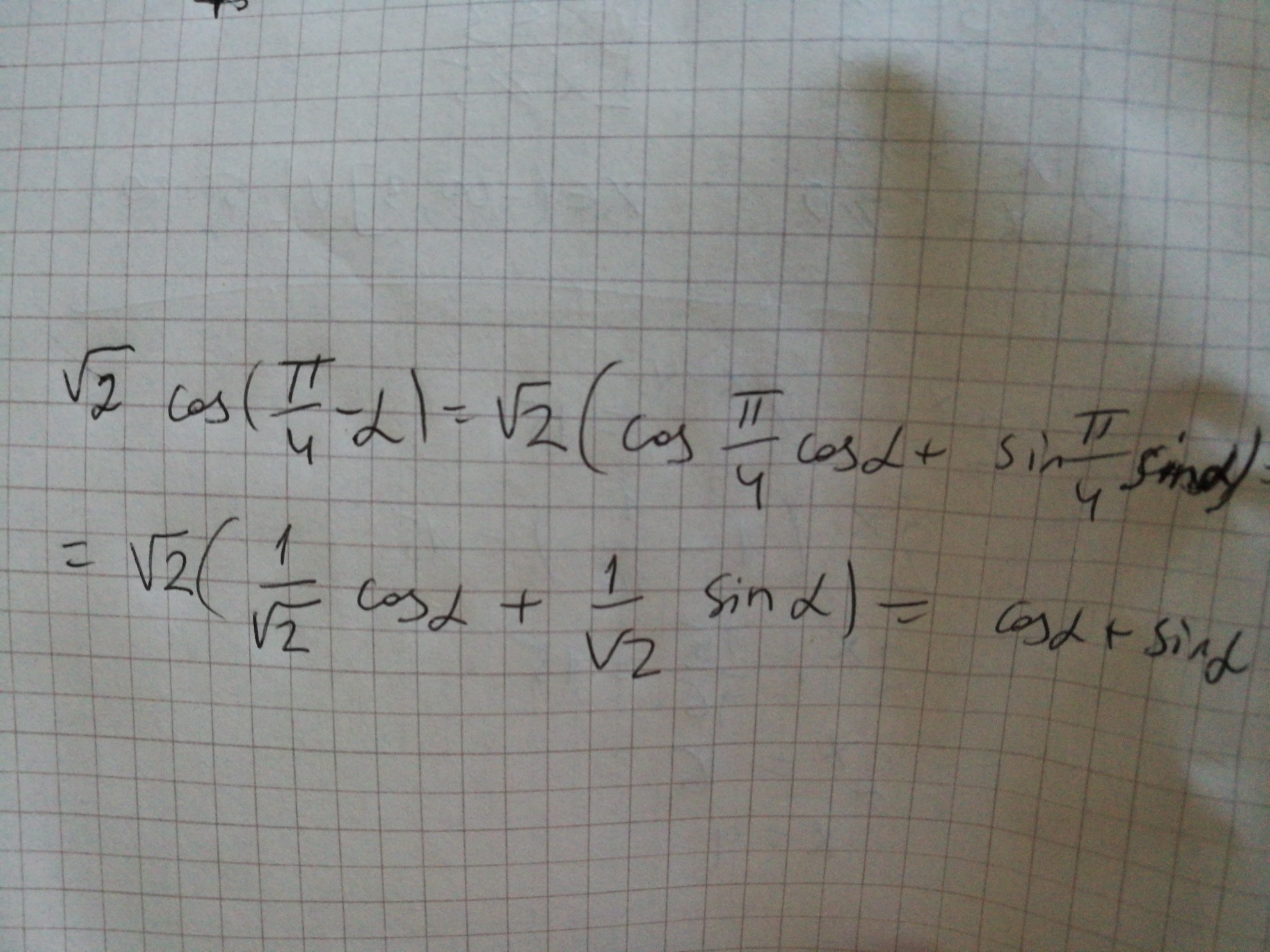
Ответ дал:
0
Это формула: введение вспомогательного угла. Выводится следующим образом:
Если есть выражение: asinα+bcosβ, то за скобку выносится выражение: √(a²+b²)
В данном случае: a=1 и b=1, тогда за скобку выносим √(1²+1²)=√2

Зная, что cos(π/4)=1/√2 и sin(π/4)=1/√2

Теперь сворачиваем это выражение по формуле косинуса разности:
cosα*cosβ+sinα*sinβ =cos(α-β)

И наконец, так как косинус - четная функция, то выражение в скобках можно домножить на -1, то есть

Сокращенное доказательство:

Если есть выражение: asinα+bcosβ, то за скобку выносится выражение: √(a²+b²)
В данном случае: a=1 и b=1, тогда за скобку выносим √(1²+1²)=√2
Зная, что cos(π/4)=1/√2 и sin(π/4)=1/√2
Теперь сворачиваем это выражение по формуле косинуса разности:
cosα*cosβ+sinα*sinβ =cos(α-β)
И наконец, так как косинус - четная функция, то выражение в скобках можно домножить на -1, то есть
Сокращенное доказательство:
Приложения:
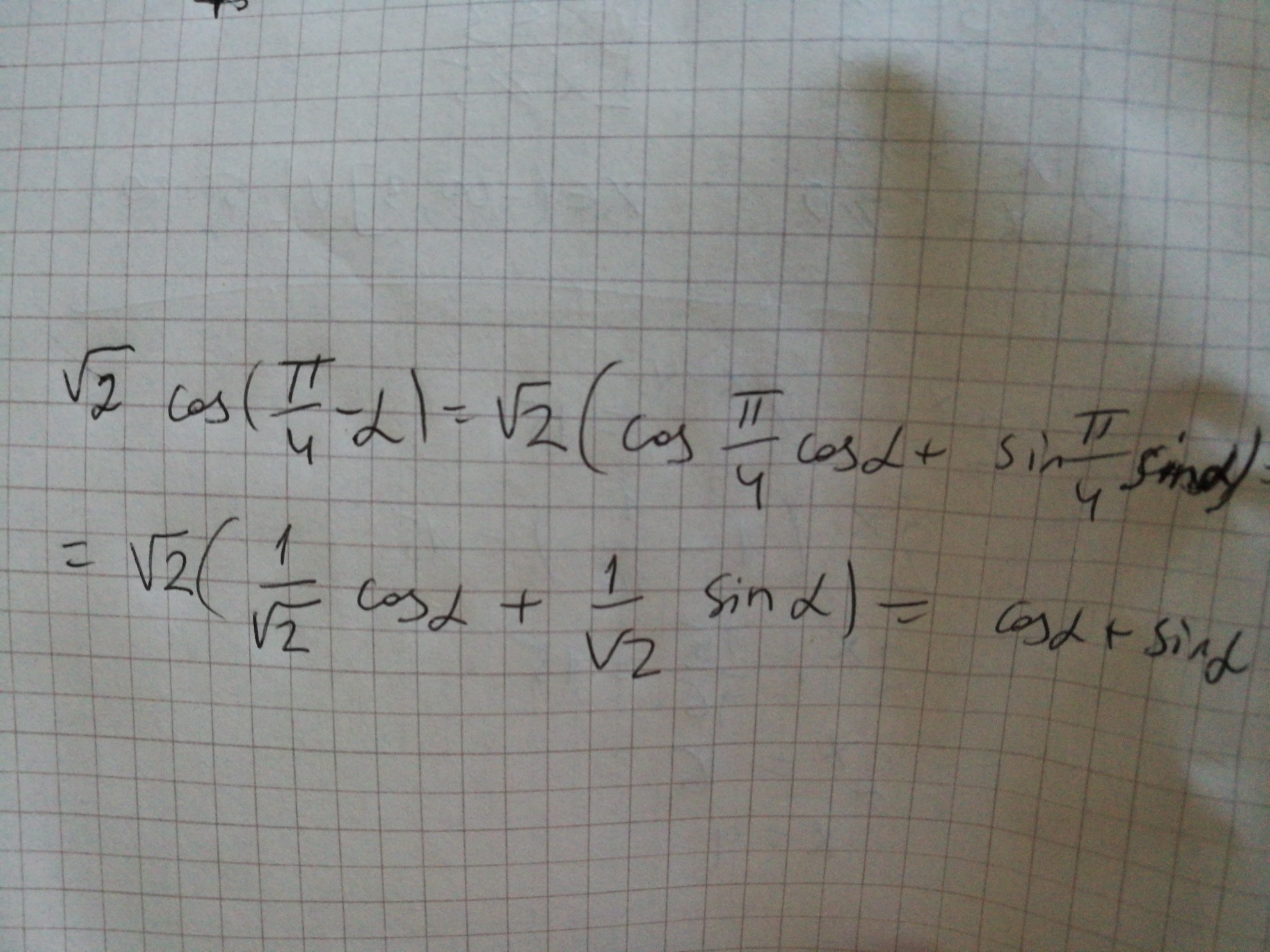
Вас заинтересует
2 года назад
2 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад