Помогите решить уравнение.
sin4 2x + cos4 2x = 5/8
В ответе указать ( в градусах) число корней на промежутке [0; 180] градусов.
Приложения:
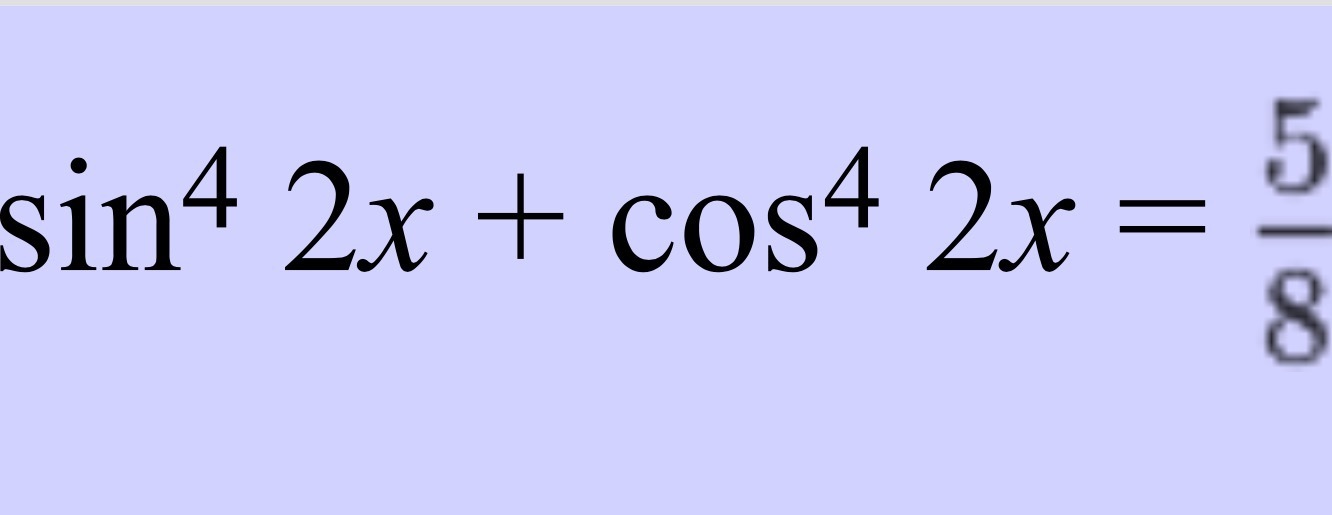
Ответы
Ответ дал:
0
Пусть 2x = t ⇒
Используем формулы понижения степени
Для отбора корней на [0°; 180°] запишем в градусах: х = ±15°+45°k, k∈Z.
1) 15°+45°k, k∈Z ⇒ k=0;1;2;3 - 4 корня
2) -15°+45°k, k∈Z ⇒ k=1;2;3;4 - 4 корня
Итого 8 корней на [0°; 180°]
Ответ: 8
Приложения:

Ответ дал:
0
sin⁴2x+cos⁴2x=5/8
(sin²2x+cos²2x)-2*sin²2x*cos²2x=5/8
1-(sin²4x)/2=5/8
2-sin²4x=5/4
sin²4x=2-5/4
sin²4x=3/4
(1-cos8x)/2=3/4
1-cos8x=3/2
cos8x=1-3/2
cos8x=-1/2
8x=±2π/3+2πk
x=±π/12++πk/4
x=±15°+45°k
0≤x≤180°
0≤15°+45°k≤180°
-15°≤45°k≤165°
-1/3≤k≤3,7
k={0;1;2;3;}
x={15°;60°;105°;150°}
0≤-15°+45k≤180°
15°≤45°k<195°
1/3≤k≤4,3
k={1;2;3;4}
x={30°;75°;120°;165°}
ответ 8 корень
(sin²2x+cos²2x)-2*sin²2x*cos²2x=5/8
1-(sin²4x)/2=5/8
2-sin²4x=5/4
sin²4x=2-5/4
sin²4x=3/4
(1-cos8x)/2=3/4
1-cos8x=3/2
cos8x=1-3/2
cos8x=-1/2
8x=±2π/3+2πk
x=±π/12++πk/4
x=±15°+45°k
0≤x≤180°
0≤15°+45°k≤180°
-15°≤45°k≤165°
-1/3≤k≤3,7
k={0;1;2;3;}
x={15°;60°;105°;150°}
0≤-15°+45k≤180°
15°≤45°k<195°
1/3≤k≤4,3
k={1;2;3;4}
x={30°;75°;120°;165°}
ответ 8 корень
Приложения:

Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
10 лет назад