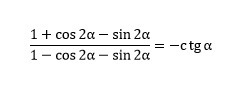Question

докажите тождество, пожалуйста.

Answer 1

$displaystyle frac{1+cos2alpha-sin2alpha}{1-cos2alpha-sin2alpha}=frac{cos^2alpha+sin^2alpha+cos^2alpha-sin^2alpha-2sinalphacosalpha}{cos^2alpha+sin^2alpha-cos^2alpha+sin^2alpha-2sinalphacosalpha}=\ \ =frac{2cos^2alpha-2sinalphacosalpha}{2sin^2alpha-2sinalphacosalpha}=-frac{2cosalpha(cosalpha-sinalpha)}{2sinalpha(cosalpha-sinalpha)}=-frac{2cosalpha}{2sinalpha}=-mathrm{ctg} alpha$

Answer 2

Решение поправил

Answer 3

1) Упростим числитель:

1+cos(2α)-sin(2α)=sin²α+cos²α+cos²α-sin²α-2*sinα*cosα=2*cos²α-2*sinα*cosα=

=2*cosα*(cosα-sinα).

2) Упростим знаменатель:

1-cos(2α)-sin(2α)=sin²α+cos²α-cos²α+sin²α-2*sinα*cosα=2*sin²α-2*sinα*cosα=

=2*sinα*(sinα-cosα)=-2*sinα*(cosα-sinα).

3) Разделим числитель на знаменатель:

2*cosα*(cosα-sinα)/(-2*sinα*(cosα-sinα)=-cosα/sinα=-ctgα.

Тождество доказано.