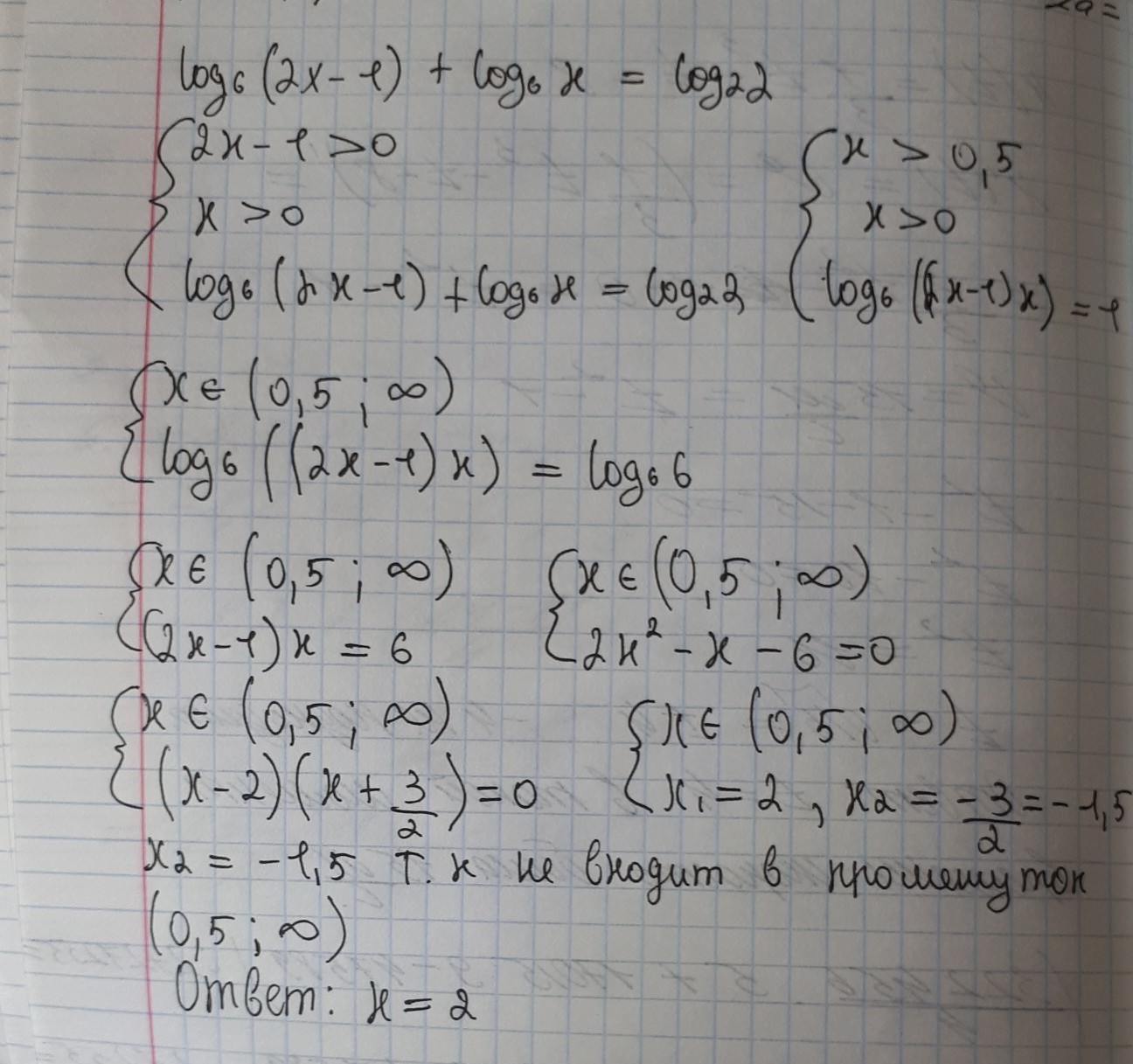Question

Кто сможет решить? Буду очень благодарна!!!

Answer 1

Решение на фото .........

Answer 2

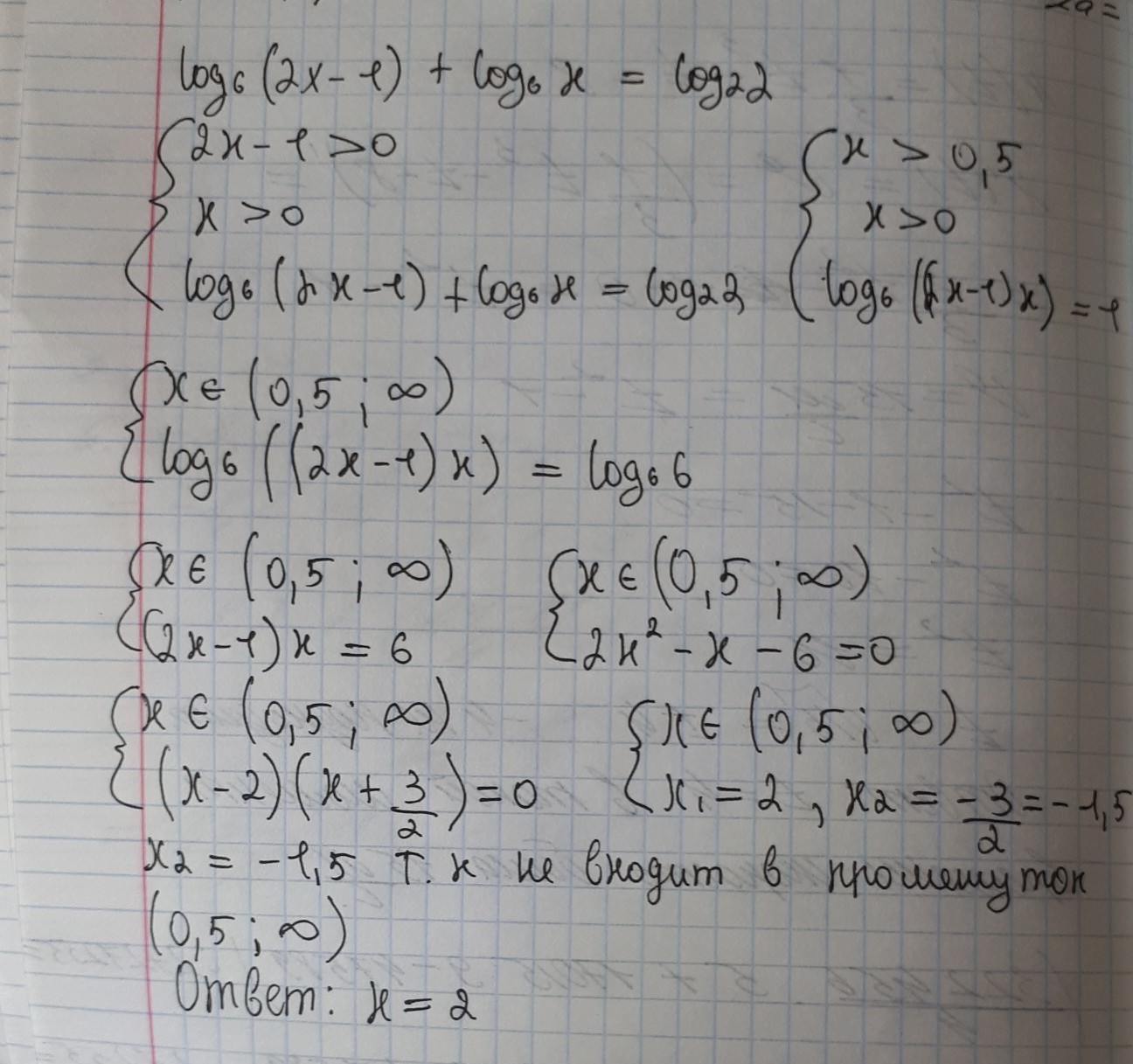
3.

Найдём область допустимых значений(ОДЗ):

x∈($frac{1}{2}$,∞);

Упростить выражение,используя формулу ㏒ₐ(x)+㏒ₐ(y)=㏒ₐ(x+y):

㏒₆((2x-1)x)=㏒₂(2);

Логарифм с одинаковым основанием и аргументом=1:

㏒₆((2x-1)x)=1;

Распределить x через скобки:

㏒₆(2x²-x)=1;

Выражение ㏒ₐ(x)=b равносильно x=aᵇ:

2x²-x=6¹;

Любое выражение,возведённое в степень 1=самому себе:

2x²-x=6;

Перенести константу в левую часть и изменить её знак на противоположный:

2x²-x-6=0;

Решить квадратное уравнение вида ax²+bx+c=0,используя формулу $x=frac{-b+-sqrt{b^{2}-4ac}}{2a}$

$x=frac{-(-1)+-sqrt{(-1)^{2}-4*2*(-6)}}{2*2}$;

Когда перед скобками есть знак "-",знак каждого члена в скобках нужно изменить на противоположный:

$x=frac{1+-sqrt{(-1)^{2}-4*2*(-6)}}{2*2}$;

Вычислить степень:

$x=frac{1+-sqrt{1-4*2*(-6)}}{2*2}$;

Использовать правила умножения для вычисления выражения;умножить числа в знаменателе:

$x=frac{1+-sqrt{1+48}}{4}$;

Сложить числа:

$x=frac{1+-sqrt{49}}{4}$;

Вычесть квадратный корень:

$x=frac{1+-7}{4}$;

Отделить решения:

$x=frac{1+7}{4}$

$x=frac{1-7}{4}$;

Упростить выражение:

x=2

x=$-frac{3}{2}$, x∈($frac{1}{2}$,∞);

Проверить,принадлежит ли решение заданному интервалу:

x=2

4.

Найти область допустимых значений(ОДЗ):

x≠3;

Перенести константу в левую часть и изменить её знак на противоположный:

$frac{2}{x-3}+1 leq 0$;

Записать все числители над общим знаменателем:

$frac{2+x-3}{x-3} leq 0$;

Вычислить разность:

$frac{-1+x}{x-3} leq 0$;

Существует два случая,при которых частное $frac{a}{b}$ может быть ≤0 $left { {{a leq 0} atop {b textgreater 0}} right.$ или $left { {{a geq 0} atop {b textless 0}} right.$:

$left { {{-1+x leq 0} atop {x-3 textgreater 0}} right. \ left { {{-1+x geq 0} atop {x-3 textless 0}} right.$

Решить неравенство относительно x:

$left { {{x leq 1} atop {x textgreater 3}} right. \ left { {{x geq 1} atop {x textless 3}} right.$

Найти пересечение:

x∈∅

x∈[1,3);

Найти объединение:

x∈[1,3), x≠3;

Найти пересечение множества решений и области допустимых значений:

x∈[1,3)

Ответ:3)1+2=3.

Answer 3

спасибо огромное!

Answer 4

На кнопку выше нажми