Question

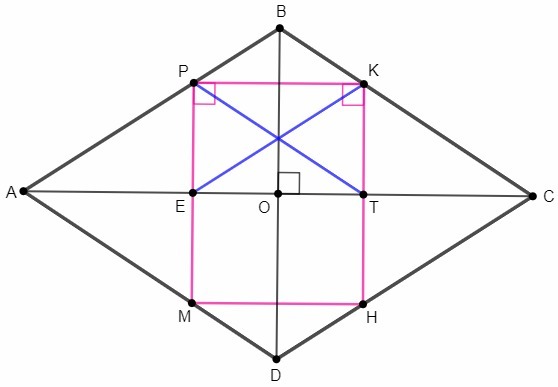
12) На сторонах AB, BC, CD и AD ромба ABCD взяты точки P, K, H, M соответственно. Каждая из прямых PM, KH, PK параллельна одной из осей симметрии ромба. Диагональ AC пересекает отрезок PM в точке E, а отрезок KH в точке T
а) докажите,что диагонали четырехугольника EPКT равны
б) определите вид четырёхугольника MPKH.

Answer 1

a)

1) Симметриями ромба являются его диагонали. Значит, PM || BD , KH || BD , PK || AC .

Так как PM || BD , KH || BD , то PM || KH , РK || AC

Значит, четырёхугольник EPKT - параллелограмм

По свойству ромба: диагонали ромба взаимно перпендикулярны =>

AC перпендикулярно BD

К тому же PM || BD , KH || BD

Значит, отрезки KH и PM перпендикулярны отрезку AC

PK || AC, KH || PM , KH и PM перпендикулярны отрезку AC

Из всего этого следует, что параллелограмм EPKT является прямоугольником

По свойству прямоугольника:

Диагонали прямоугольника равны, что и требовалось доказать

б)

Так как ромб - это симметричная фигура
следует, что относительно диагоналей AC и ВD происходит симметрия =>

∆ ABC = ∆ АСD

Из первого пункта было сказано, что EPKT является прямоугольником

Значит, прямоугольник EPKT симметрично накладывается на четырёхугольник METH, которые вследствие симметричности является также прямоугольником. А значит, весь четырехугольник МРKH является прямоугольником.

Для точности докажем, что точки Р и М, К и Н симметричны относительно диагонали АС

∆ АРЕ = ∆ АЕМ - по катету и острому углу ( угол ВАС = угол САD - по свойству ромба ; АЕ - общая сторона )
Значит, РЕ = ЕМ

Аналогично доказывается, что КТ = ТН . Поэтому точки Р и К соответственно симметричны точкам М и Н относительно диагонали АС.

ОТВЕТ: прямоугольник

Answer 2

Диагональ АС и BD делят ромб на две попарно симметричные фигуры: ∆ АВС = ∆ АDC. Прямоугольник EPKT симметрично накладывается на четырёхугольник МЕТН, который вследсвие симметричности явл. прямоугольником. Теперь уж доказано. Видно, что задача на симметрию.

Answer 3

Диагональ ВD пересекает PK и MH в точках F и N. Аналогично ∆ ABD = ∆ BCD . Прямоугольник MPFN симметрично накладывается на прямоугольник FKHN.

Answer 4

Прямоугольник EPKN наложится куда надо, когда будет доказано, что M симметрична P и H симметрична K. Как это доказано?
Например. Точка В симметрична точке D относительно AC, так как известно, что BD⊥AC, O∈AС, BO=OD.

Answer 5

Зачем к мелочям предираетесь? Вами сказано, что В симметрична D. А так как РМ || ВD, точка P симметрична точки М. Или по другому : Видно, что PE = EM из равенства прям. треугольников

Answer 6

Уже все сказано благодаря СИММЕТРИЧНОСТИ!

Answer 7

Ромб ABCD симметричен относительно диагоналей AC, BD.

PM || BD || KH, PK||AC

(Если точки находятся по разные стороны от диагонали, то, очевидно, отрезок, соединяющий точки, пересекает диагональ и не может быть ей параллелен.)

1) Диагонали ромба перпендикулярны, AC⊥BD. Прямые, параллельные перпендикулярным, перпендикулярны*, PM⊥AC, KH⊥AC, PK⊥BD. Смежные стороны EPKT лежат на перпендикулярных прямых, EPKT - прямоугольник. Диагонали прямоугольника равны.

2) Стороны ромба равны, диагональ делит ромб на равнобедренные треугольники. Прямая, параллельная диагонали, отсекает подобный равнобедренный треугольник, PB=BK, MA=AP, KC=CH. Из равных длин вычитаем равные, AP=KC. Противоположные углы ромба равны, MA=AP=KC=CH => △MAP и △KCH равны по двум сторонам и углу между ними, PM=KH. MPKH - параллелограмм (противоположные стороны равны и параллельны). PM||BD, PK⊥BD => PM⊥PK. Параллелограмм с прямым углом - прямоугольник.

____________________________________________________________

* Соответственные углы при параллельных равны. Если секущая пересекает одну параллельную под прямым углом, то и другую она пересекает под прямым углом.