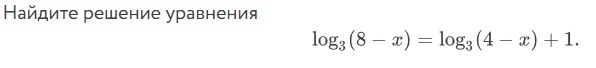Ответы
Ответ дал:
0
1)
![{2}^{ log_{8}(3x - 4) } = 5 \ {2}^{ log_{ {2}^{3} }(3x - 4) } = 5 \ {2}^{ frac{1}{3} log_{2}(3x - 4) } = 5 \ {2}^{ log_{2} {(3x - 4)}^{ frac{1}{3} } } = 5 \ {2}^{ log_{2}( sqrt[3]{3x - 4} ) } = 5 \ sqrt[3]{3x - 4} = 5 \ 3x - 4 = {5}^{3} \ 3x - 4 = 125 \3 x = 129 \ x = 43 {2}^{ log_{8}(3x - 4) } = 5 \ {2}^{ log_{ {2}^{3} }(3x - 4) } = 5 \ {2}^{ frac{1}{3} log_{2}(3x - 4) } = 5 \ {2}^{ log_{2} {(3x - 4)}^{ frac{1}{3} } } = 5 \ {2}^{ log_{2}( sqrt[3]{3x - 4} ) } = 5 \ sqrt[3]{3x - 4} = 5 \ 3x - 4 = {5}^{3} \ 3x - 4 = 125 \3 x = 129 \ x = 43](https://tex.z-dn.net/?f=+%7B2%7D%5E%7B+log_%7B8%7D%283x+-+4%29+%7D+%3D+5+%5C+%7B2%7D%5E%7B+log_%7B+%7B2%7D%5E%7B3%7D+%7D%283x+-+4%29+%7D+%3D+5+%5C+%7B2%7D%5E%7B+frac%7B1%7D%7B3%7D+log_%7B2%7D%283x+-+4%29+%7D+%3D+5+%5C+%7B2%7D%5E%7B+log_%7B2%7D+%7B%283x+-+4%29%7D%5E%7B+frac%7B1%7D%7B3%7D+%7D+%7D+%3D+5+%5C+%7B2%7D%5E%7B+log_%7B2%7D%28+sqrt%5B3%5D%7B3x+-+4%7D+%29+%7D+%3D+5+%5C+sqrt%5B3%5D%7B3x+-+4%7D+%3D+5+%5C+3x+-+4+%3D+%7B5%7D%5E%7B3%7D+%5C+3x+-+4+%3D+125+%5C3+x+%3D+129+%5C+x+%3D+43)
Ответ: 43.
2)

Проверка:
log_3(8 - 2) = log_3(4 - 2) + 1
log_3(6) = log_3(2) + log_3(3)
log_3(6) = log_3(6) -- верно => х = 2 является корнем уравнения.
Ответ: 2.
Ответ: 43.
2)
Проверка:
log_3(8 - 2) = log_3(4 - 2) + 1
log_3(6) = log_3(2) + log_3(3)
log_3(6) = log_3(6) -- верно => х = 2 является корнем уравнения.
Ответ: 2.
Ответ дал:
0
ОДЗ не пишем?
Ответ дал:
0
Здесь ОДЗ не нужно писать...
Ответ дал:
0
В первом номере не нужно писать ОДЗ. А вот во втором номере следует, но всё равно видно, что в результате получится линейное уравнение с одним корнем, который можно легко проверить.
Ответ дал:
0
это вам видно, а ученику - вряд ли.....
Ответ дал:
0
Не надо видеть, нужно решить и сделать проверку...
Ответ дал:
0
ОТВЕТ: 43
Проверка:
log( 3 )_( 8 - 2 ) = log( 3 )_( 4 - 2 ) + 1
log( 3 )_( 6 ) = log( 3 )_( 2 ) + log( 3 )_( 3 )
log( 3 )_( 6 ) = log( 3 )_( 6 )
Верно
ОТВЕТ: 2
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад
10 лет назад