острые углы прямоугольного треугольника равны 24° и 66°. найдите угол между высотой и медианой, проведенными из вершины прямого угла. ответ дайте в градусах.
помогите, пж, заранее спасибо
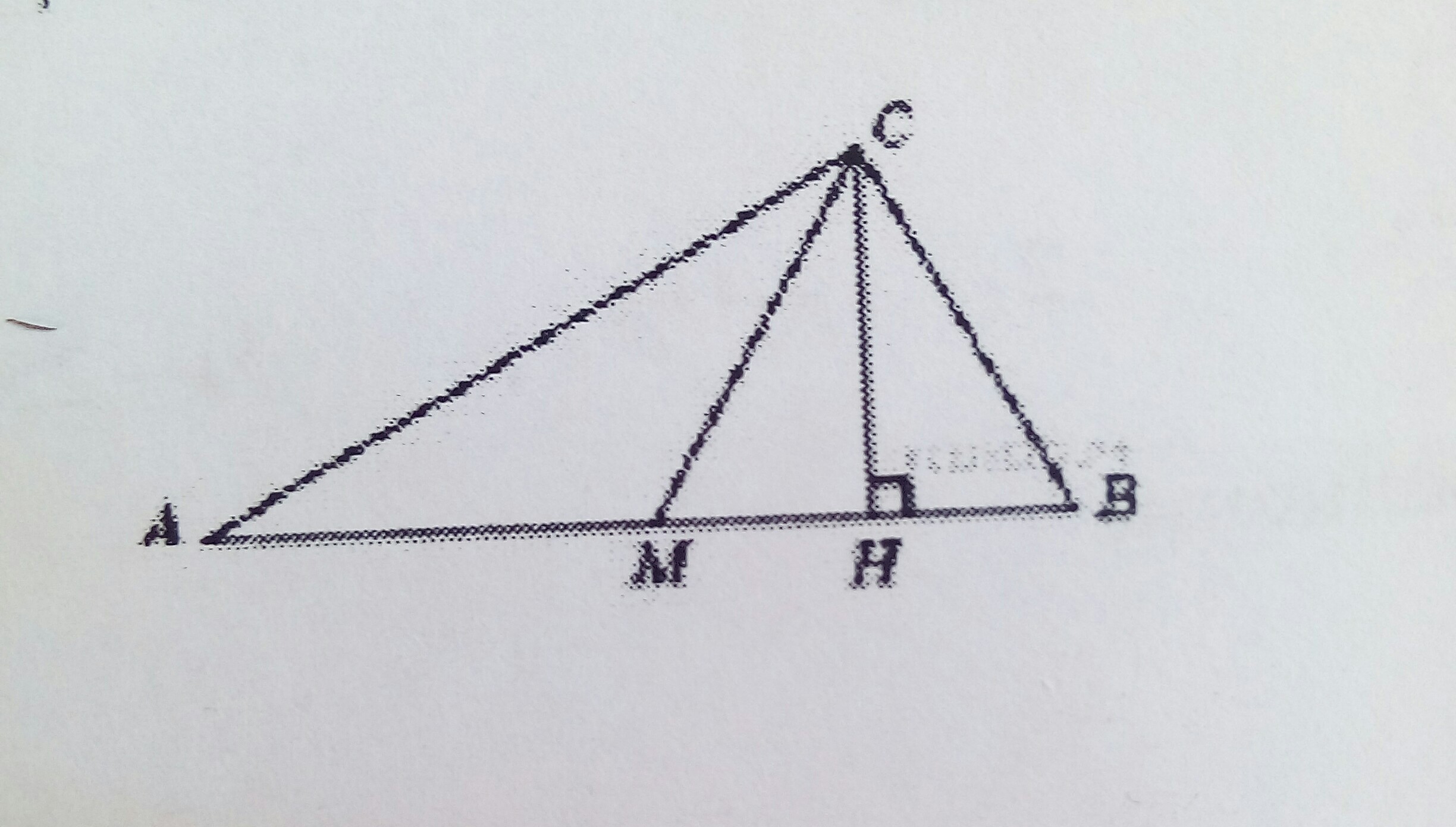
Приложения:
Ответы
Ответ дал:
0
По свойству прямоугольного треугольника:
посредине гипотенузы лежит центр описанной окружности этого треугольника.
Значит точка М - центр описанной окружности треугольника ABC. Значит AM = MC = MB = радиус окружности.
Следовательно треугольник AMC равнобедренный. угол ACM = угол CAM = 24°
угол HCB = 180° - 90° - 66° = 24°
угол MCH = угол ACB - угол ACM - угол HCB = 90° - 24° - 24° = 42°
Ответ: угол между медианой и высотой равен 42°
посредине гипотенузы лежит центр описанной окружности этого треугольника.
Значит точка М - центр описанной окружности треугольника ABC. Значит AM = MC = MB = радиус окружности.
Следовательно треугольник AMC равнобедренный. угол ACM = угол CAM = 24°
угол HCB = 180° - 90° - 66° = 24°
угол MCH = угол ACB - угол ACM - угол HCB = 90° - 24° - 24° = 42°
Ответ: угол между медианой и высотой равен 42°
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
10 лет назад