Ответы
Ответ дал:
0
Решение во вложении.
Приложения:

Ответ дал:
0
если сделать замену: х²-8х+18=t, то можно увидеть, что левая часть примет вид: t²-8t+18
то есть структура левой части не поменялась, поэтому данное уравнение относится к виду:
Для решения таких уравнений, есть теорема:
Уравнение f(f(x))=x, имеет такие же корни, что и уравнение f(x)=x
поэтому решим сначала уравнение:
Теперь раскроем скобки исходного уравнения:
и разделим столбиком на:
(см. рисунок)
получается
Таким образом, корни уравнения:
равны
Сумма целых решений:
3+6=9
Ответ: 9
Приложения:
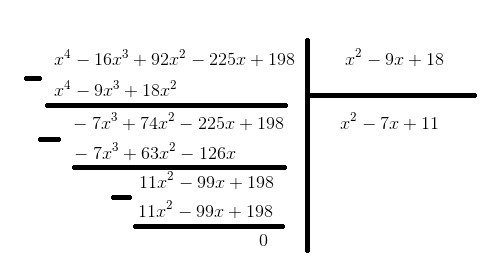
Вас заинтересует
2 года назад
2 года назад
3 года назад
9 лет назад
10 лет назад
10 лет назад