Question

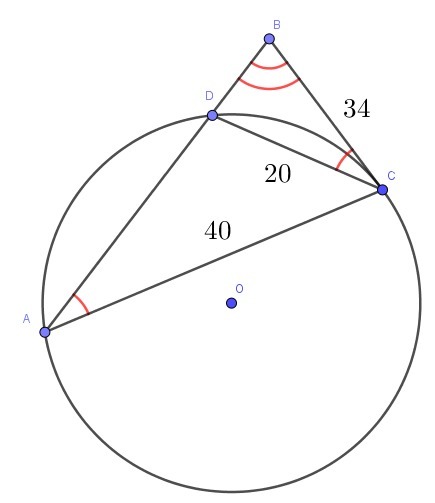
На сто­ро­не AB тре­уголь­ни­ка ABC взята точка D так, что окружность, про­хо­дя­щая через точки A, C и D, ка­са­ет­ся пря­мой BC. Най­ди­те AD, если AC = 40, BC = 34 и CD = 20.

Answer 1

Если окружность касается прямой ВС и проходит через точку С, то С - точка касания:

угол между касательной и хордой равен половине заключенной дуги:

$angle BCA=frac{1}{2}breve{CD}$

∠DAC - вписанный, значит:

$angle DAC=frac{1}{2}breve{CD}$

Отсюда:

$angle BCA=angle DAC$

Для треугольников АВС и DBC: ∠В - общий ⇒ они подобны по двум углам

$Delta ABC sim Delta DBC$

Значит справедливы равенства:

$frac{BC}{BD} =frac{AB}{BC}=frac{AC}{CD} \ \ frac{34}{BD}=frac{AB}{34} =frac{40}{20}=2 \ \ AB=2*34=68 \ BD=frac{34}{2}=17 \ \ AD=AB-BD=68-17=51 \ \ OTBET: 51$