Question

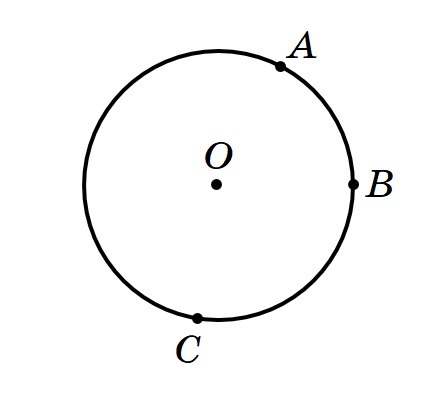
Окружность с центром в точке О разделена точками А, В и С на дуги, длины которых относятся как 3 : 5 : 10 (см. рисунок). Сколько процентов всей окружность составляет дуга ВС?

Answer 1

Всего частей 3+5+10=18 =100%, средняя по размеру дуга ВС=5 частей =х%, х=5*100/18≈27.8% -ответ

Answer 2

Почему?

Answer 3

Спасибо

Answer 4

Почему ВС = 5 частей?

Answer 5

Согласно размерам по рисунку в порядке 3<5<10

Answer 6

Можно еще провести радиусы и сопоставить углы

Answer 7

Дано: AB : BC : CA = 3 : 5 : 10

Найти: P(BC) - ?

Решение. Полная окружность, имеющая процентное отношение 100 % равна: 3 + 5 + 10 = 18, то есть эта окружность разделена на 18 равных частей, из которых дуга ВС занимает 5 таких частей.

Составим пропорцию, где P(BC) - это процентное отношение дуги BC от всей окружности:

18 - 100 %

5 - P(BC)

Или:

$dfrac{18}{5} = dfrac{100 %}{P(BC)}$. Отсюда $P(BC) = dfrac{5 cdotp 100 %}{18} = dfrac{500 %}{18} approx 27,78 %$

Answer 8

500 на 18 нацело не делится, поэтому точным (целым) быть не может. Вот если бы требовалось в градусах, то 5*360/18=100° -целое

Answer 9

Никита, еще округлить бы по правилам:)

Answer 10

Округлить до десятых? Или написать в периоде?

Answer 11

Хех, да как изволите, только если до целых, будет ≈28 :)

Answer 12

А если до десятков, то будет ≈30 :(