Question

Очень нужна помощь!!! Нужно решить задачу по рисунку

Answer 1

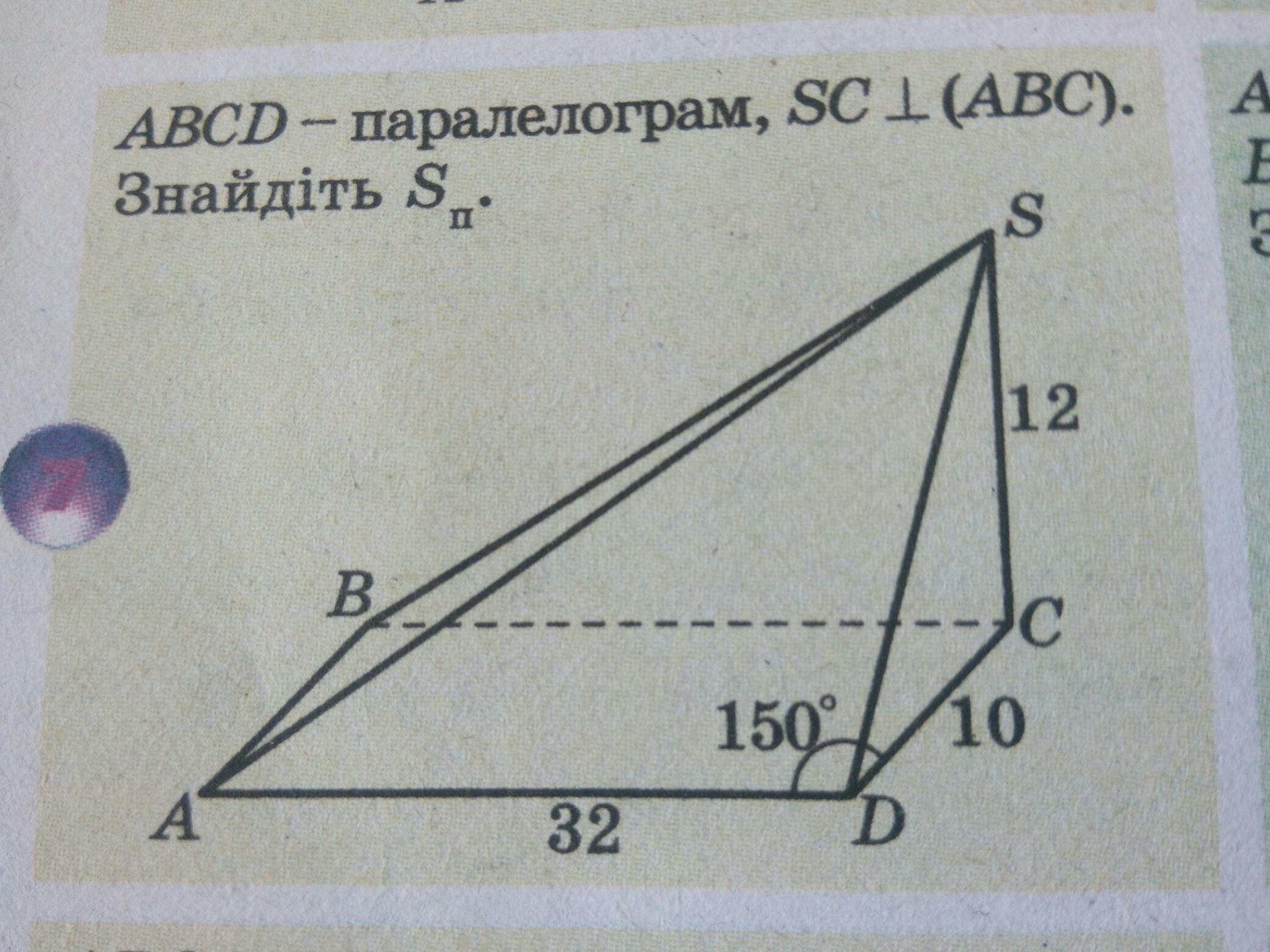
• SC перпендикулярен ( АВС )
Если прямая перпендикулярна к плоскости, то она перпендикулярна любой прямой, лежащей в этой плоскости.
SC перпендикулярен CD
SC перпендикулярен CD
Отсюда, тр. SCD и SCB - прямоугольные.
• Также SC перпендикулярен АС =>
тр. SCA - прямоугольный
• Рассмотрим тр. АDC:
По теореме косинусов:
АС^2 = АD^2 + DC^2 - 2 • AD • DC • cos150°
AC^2 = 32^2 + 10^2 - 2 • 32 • 10 • ( - /3 / 2 )
AC^2 = 1024 + 100 + 320/3
AC^2 = 1124 + 320/3
AC =
$= sqrt{1124 + 320 sqrt{3} } = 2 sqrt{281 + 80 sqrt{3} }$
• Рассмотрим тр. SCA (угол SCA = 90°):
По теореме Пифагора:
АS^2 = AC^2 + SC^2
AS^2 = 1124 + 320/3 + 144 = 1268 + 320/3
AS =
$= sqrt{1268 + 320 sqrt{3} } = 2 sqrt{317 + 80 sqrt{3} }$
• Рассмотрим тр. SCD (угол SCD = 90°):
По теореме Пифагора:
SD^2 = CD^2 + SC^2
SD^2 = 12^2 + 10^2
SD^2 = 144 + 100 = 244
SD = 2/61
• Рассмотрим тр. SCB (угол SCB = 90°):
По теореме Пифагора:
ВS^2 = BC^2 + SC^2
BS^2 = 32^2 + 12^2
BS^2 = 1024 + 144 = 1168
BS = 4/73
● Рассмотрим тр. АSD:
Данный треугольник произвольный, найдём её площадь следующим образом:
По теореме косинусов:
Распишу кратко:
АС^2 = АD^2 + CD^2 - 2 • AD • CD • cos АDC
1268 + 320/3 = 1024 + 244 - 2 • 32 • 2/61 • cos ADC
cos ADC =
$= - frac{320 sqrt{3} }{2 times 32 times 2 sqrt{61} } = - frac{5 sqrt{3} }{2 sqrt{61} }$
• Теперь найдём синус этого же угла через основное тригонометрическое тождество:

$sin : : adc = sqrt{1 - : {(cos : : adc)}^{2} } = sqrt{1 - frac{25 times 3}{4 times 61} } = \ = sqrt{ frac{4 times 61 - 25 times 3}{4 times 61} } = sqrt{ frac{169}{4 times 61} } = frac{13}{2 sqrt{61} }$

• S adc = ( 1/2 ) • AD • CD • sin ADC =
$= frac{1}{2} times 32 times 2 sqrt{61} times frac{13}{2 sqrt{61} } = frac{1}{2} times 32 times 13 = \ = 16 times 13 = 208$

● Рассмотрим тр. АВS:
Найдем её площадь таким же способом.
По теомере косинусов:
АS^2 = AB^2 + BS^2 - 2 • AB • BS • cos ABS
1268 + 320/3 = 1168 + 100 - 2 • 4/73 • 10 • cos ABS
cos ABS =
$= - frac{320 sqrt{3} }{2 times 4sqrt{73} times 10} = - frac{4 sqrt{3} }{ sqrt{73} }$
• Теперь найдём синус этого же угла через основное тригонометрическое тождество:

$sin : abs = sqrt{1 - {(cos : abs) }^{2} } = sqrt{1 - frac{16 times 3}{73} } = \ = sqrt{ frac{73 - 48}{73} } = sqrt{ frac{25}{75} } = frac{5}{ sqrt{73} }$

• S abs = ( 1/2 ) • AB • BS • sin ABS =
$= frac{1}{2} times 10 times 4 sqrt{73} times frac{5 }{ sqrt{73} } = frac{1}{2} times 10 times 4 times 5 = \ = 100$

• S scd = ( 1/2 ) • 12 • 10 = 60
• S scb = ( 1/2 ) • 12 • 32 = 192


● S пол.пов. = S scd + S scb + S abs + S ads = 60 + 192 + 100 + 208 = 560



ОТВЕТ: 560