Question

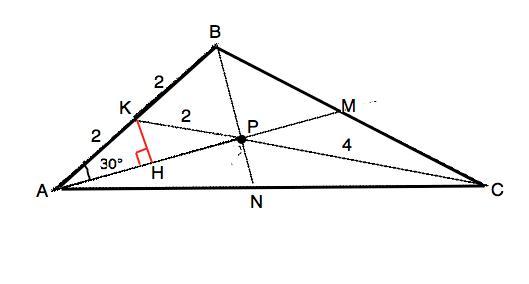
Медианы am и bn в треугольнике abc пересекаются в точке p. Известно, что ab=cp=4. Кроме того, угол PAB= 30 градусам, найдите длину отрезка PM

Answer 1

ишу сразу ответ: 1) я не знаю, изучали вы корни или нет, но ответ таков: x=r 2) первый х равен 2, второй х равен -1/2 3) первый х равен 24, второй х равен 3

так или

376х =8 х=376: 8 х= 47 477х=9 х=477 : 9 х=53 777х=3 х= 777 : 3 х= 259

Answer 2

Ответ: РМ=√3

Объяснение:  

Медианы треугольника пересекаются в одной точке. Следовательно, отрезок СР - часть медианы из С, Продолжим ее до пересечения с АВ в точке К.

  Медианы треугольника точкой пересечения делятся в отношении 2:1, считая от вершины. ⇒ РК=СР:2=4:2=2.

Точка К - середина АВ. ⇒

АК=КВ=2.

 Треугольник АКР равнобедренный ( АК=КР).  

Из К опустим высоту КН на АР. Отрезок КН=АК:2=1 (свойство катета, противолежащего углу 30°).

Тогда АН=НР=КН•ctg30°=√3 ⇒ АР=2√3

По свойству медиан АР:РМ=2:1, поэтому РМ=0.5•2√3=√3