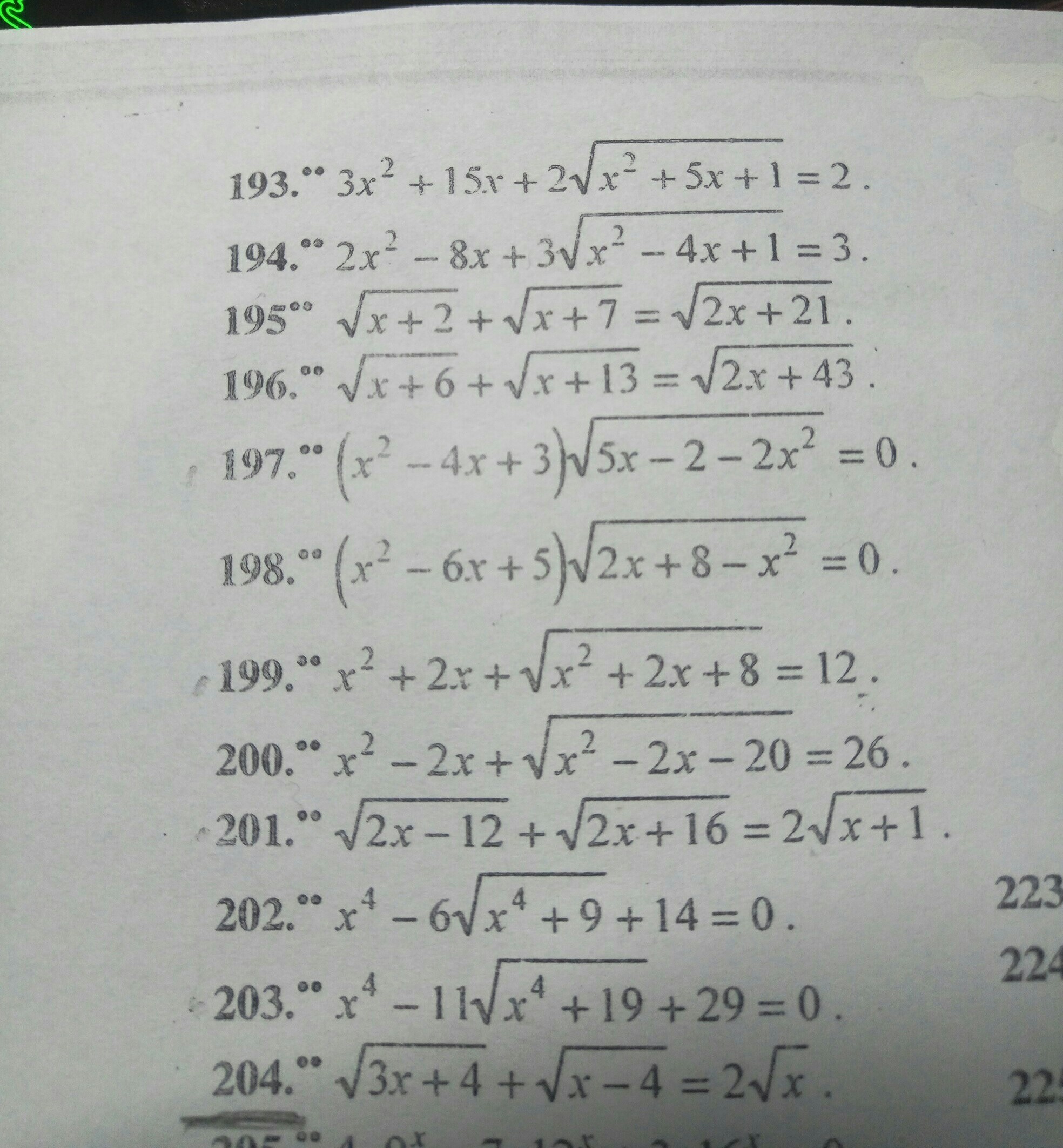Ответы
Ответ дал:
0
На фотографии отмечен 204 номер. Отсюда беру вывод, что нужен именно он. В пояснениях ничего не написано.
Решение уравнения.

Рассмотрим все случаи:


Проверяем решение:


Отсюда получаем, что первое выражение не является решением:

Второе же определенно подходит:

Ответ : x = 4
Решение уравнения.
Рассмотрим все случаи:
Проверяем решение:
Отсюда получаем, что первое выражение не является решением:
Второе же определенно подходит:
Ответ : x = 4
Ответ дал:
0
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
Приложения:





Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад