Question

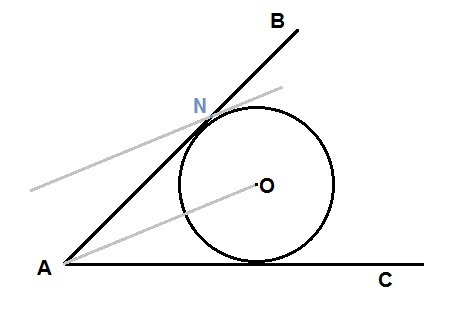
В угол BAC вписана окружность с центром О. Касательная к окружности, параллельная AO, пересекает луч AB в точке N. Найдите длину отрезка AN, если AO = 13.

Answer 1

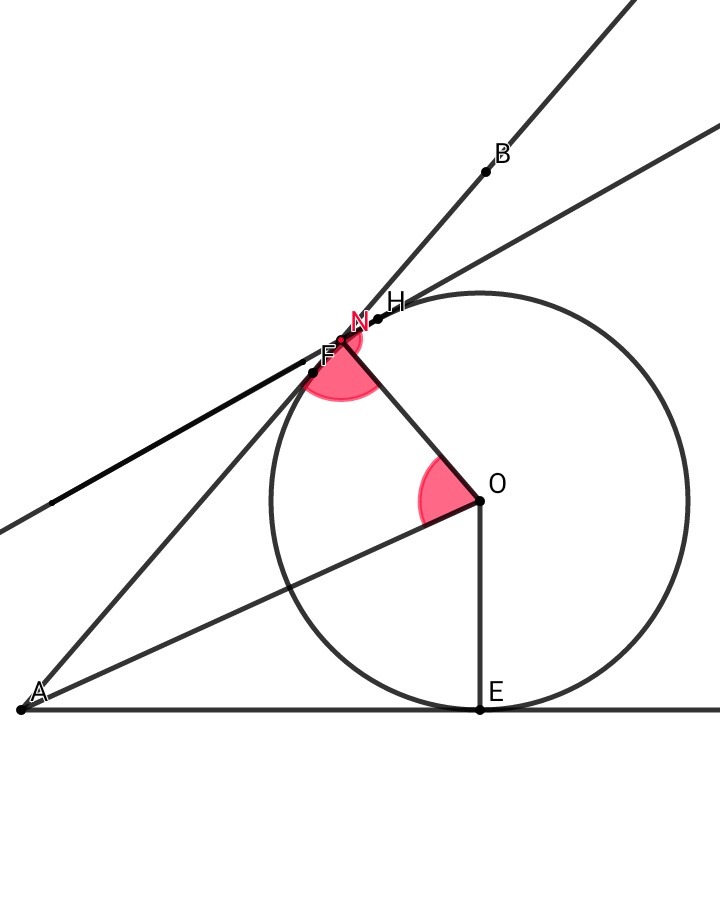
Окружность с центром О не только вписанa в угол ВАС, но она вписана и в угол АNH. Поэтому по теореме об отрезках касательных: отрезки касательных, к окружности, проведённые из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности. Следовательно, угол ANO = угол HNO. Но с другой стороны, NH || AO - по условию => угол НNO = угол АОN - как накрест лежащие углы при NH || AO и секущей NO. Отсюда угол ANO = угол AON => тр. AON - равнобедренный, AN = AO = 13

ОТВЕТ: 13