Question

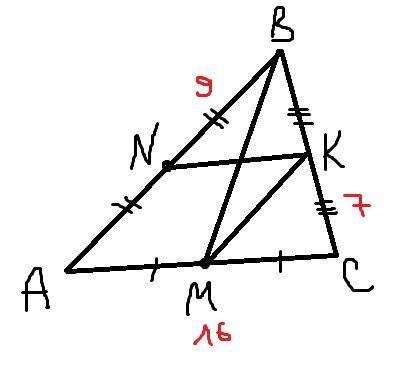
в треугольнике авс проведена медиана BM, отрезки MK паралельно BC(K принадлежит BC), KN паралельно AC(N принадлежит AB). Найдите периметр четырехугольника ANKC, если KC=7 см, AC=16 см, BN=9 см БЫСТРЕЙ!!!!!

Answer 1

AN = NB = 9 cm (средняя линия)

NK =1/2 AC = 16 cm ( средняя линия )

Pankc= 16+7+9+8=40 cm

Можешь не благодарить :)

Answer 2

Ответ:

ВМ - медиана, значит М-середина АС.

М-середина АС, МК параллелен АВ, значит К-середина ВС.

К-середина ВС, KN параллелен AC, значит  N-середина АВ.

N-середина АВ, значит АN=NВ=9.

КС=7, АС=16 -по условию.

К-середина ВС, N-середина АВ, значит NК-средняя линия и NК=АС:2=16:2=8.

Р=9+8+7+16=40.