Question

Помогите, пожалуйста, с геометрией (см. вложение)!!!

Answer 1

Прямоугольный параллелепипед — это прямая четырёхугольная призма, в основании которой прямоугольник.

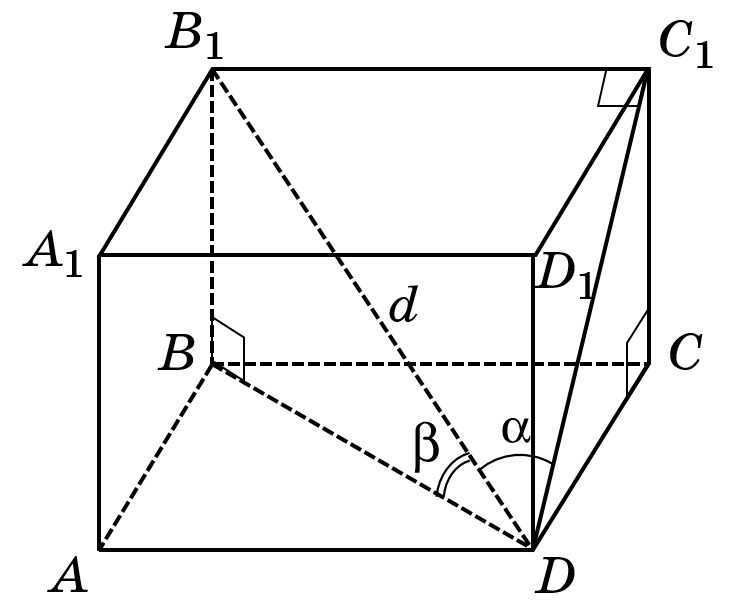
Пусть в прямоугольном параллелепипеде $ABCDA_{1}B_{1}C_{1}D_{1}$ диагональ $B_{1}D = d$ образует $angle B_{1}DC_{1} = alpha$ с боковой плоскостью $(CDD_{1})$ и $angle B_{1}DB = beta$ с плоскостью основания $(ABC)$ (см. вложение). Так как параллелепипед прямоугольный, то его основанием является прямоугольник.

Определим объём $V$ этого параллелепипеда.

Объём прямоугольного параллелепипеда определяется по формуле $V = S_{text{o}}c = abc,$ где $S_{text{o}} = ab$ — площадь основания ($a$ и $b$ — стороны прямоугольника), $c$ — высота.

Рассмотрим $Delta B_{1}BD (angle B_{1}BD = 90^{circ}):$

$BB_{1} = B_{1}D cdotp sin angle B_{1}DB = d sin beta$

По свойству прямоугольного (и прямого) параллелепипеда $AA_{1} = BB_{1} = CC_{1} = DD_{1} = dsin beta$

Так как у прямоугольного параллелепипеда боковые грани перпендикулярные, то прямые, которые находятся в этих двух плоскостях, будут тоже перпендикулярными (так как $(B_{1}C_{1}C) bot (C_{1}CD)$, где $B_{1}C_{1} in (B_{1}C_{1}C)$ и $C_{1}D in (C_{1}CD)$, то $B_{1}C_{1} bot C_{1}D$)

Рассмотрим $Delta B_{1}C_{1}D (angle B_{1}C_{1}D = 90^{circ}):$

$B_{1}C_{1} = B_{1}D cdotp sin angle B_{1}DC_{1} = dsin alpha$

По свойству прямоугольного параллелепипеда $AD = A_{1}D_{1} = B_{1}C_{1} = BC = dsin alpha$

$C_{1}D = B_{1}D cos angle B_{1}DC_{1} = dcos alpha$

Рассмотрим  $Delta C_{1}CD (angle C_{1}CD = 90^{circ}):$

$CD = sqrt{C_{1}D^{2} - CC_{1}^{2}} = sqrt{(dcos alpha)^{2} - (dsin beta)^{2}} = \ = sqrt{d^{2}cos^{2}alpha - d^{2}sin^{2}beta} = sqrt{d^{2}(cos^{2}alpha - sin^{2}beta)} =\= dsqrt{cos^{2}alpha - sin^{2}beta}$

По свойству прямоугольного параллелепипеда $AB = CD = A_{1}B_{1} = C_{1}D_{1} = dsqrt{cos^{2}alpha - sin^{2}beta}$

Следовательно, $V = AD cdotp CD cdotp DD_{1} = dsin alpha cdotp dsqrt{cos^{2}alpha - sin^{2}beta} cdotp dsin beta =\= d^{3}sin alpha sin beta sqrt{cos^{2}alpha - sin^{2}beta}$

Ответ: $d^{3}sin alpha sin beta sqrt{cos^{2}alpha - sin^{2}beta}$

Answer 2

Спасибо за решение, у меня похожая была!