Question

найдите площадь прямоугольной трапеции,большая боковая сторона которого 6√2 см,острый угол 45° и меньшее основание 4 см.

Answer 1

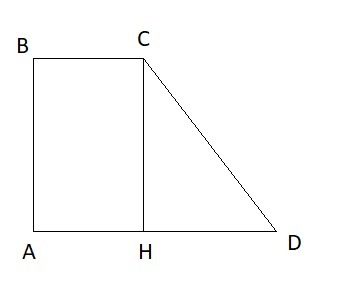
Опустим высоту CH на основание AD

ΔCHD - прямоугольный и ∠CDH = 45° ⇒ и ∠DCH = 45° и он равнобедренный. Найдем:

$CH=HD=CD*sin{45dot{}}=6sqrt{2}*frac{1}{sqrt{2}}=6$

Найдем площадь трапеции:

$S=frac{AD+BC}{2}*CH=frac{AH+HD+BC}{2}*CH=frac{HD+2*BC}{2}*CH=frac{6+2*4}{2}*6=42$

Answer 2

Здравствуй!

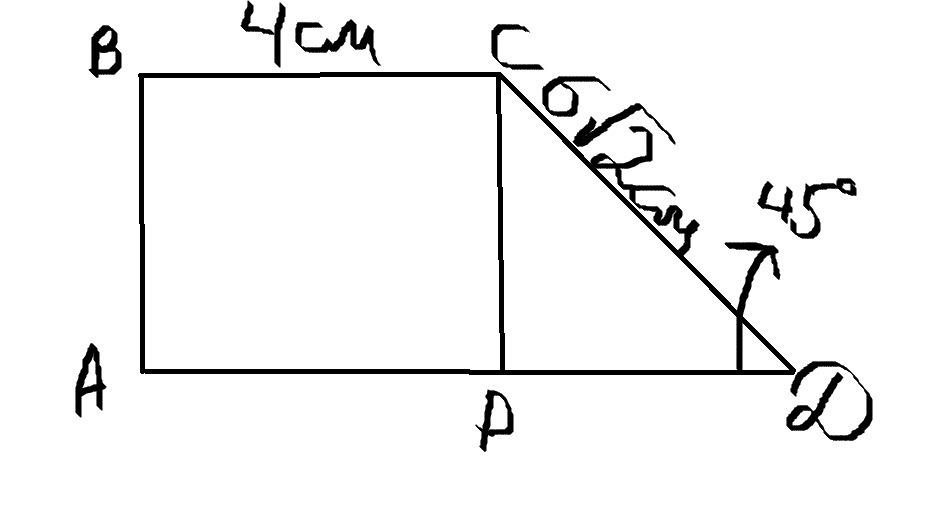
ΔСРД: ∠Д=45° ⇒ ∠С=45° ⇒ ΔСРД - равнобедренный и прямоугольный. Найдем стороны СР=РД по теореме Пифагора: пусть СР=РД=х см

$x^{2} +x^{2} =(6sqrt{2} )^{2} \x=6$

СР=РД=6 см

ВС=АР=4 см

Sтрапеции=$frac{10+4}{2} *6=42 cm^{2}$

Ответ: 42 см²

Удачи в учебе!