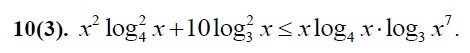Question

Решите неравенство с логарифмом

Answer 1

********************************************

Answer 2

Во первых запишем ОДЗ: x>0. Во вторых слегка преобразуем:

$x^2log_4^2x+10log_3^2xleq 7xlog_4xcdotlog_3x$

Заметим, что x=1 является решением неравенства.

Для всех x≠1 поделим обе части на положительную величину $log_3^2x$:

$frac{xlog_4x}{log_3x} -frac{7xlog_4x}{log_3x}+10leq 0$

Проводим замену:

$frac{xlog_4x}{log_3x}=t\t^2-7t+10leq 0\2leq tleq 5$

Получаем неравенство

$2leq frac{xlog_4x}{log_3x}leq 5$

Преобразуем дробь, используя свойства логарифмов:

$frac{xlog_4x}{log_3x}=frac{frac{x}{log_x 4}}{frac{1}{log_x 3}} =frac{xlog_x3}{og_x4} =xlog_4 3=frac{x}{log_3 4}$

Теперь последнее неравенство легко решается:

$2leq frac{x}{log_3 4}leq 5\2log_3 4leq xleq 5log_3 4\4log_3 2leq xleq 10log_3 2$

Единица, которую мы нашли ранее, не принадлежит этому промежутку, поэтому ее пишем в ответ отдельно.

Ответ: $x in {1} cup [4log_3 2; 10log_3 2]$

Answer 3

Куда делся квадрат если мы делим на log третей степени а там логарифм 4 степени

Answer 4

Точнее основание

Answer 5

Действительно, куда квадрат делся?)

Answer 6

Опечатка. Далее квадрат учтён.