Как решить это неравенство? (ЕГЭ, 15 вопрос)
(В объяснялке на оригинальном сайте не очень понятно)
Приложения:
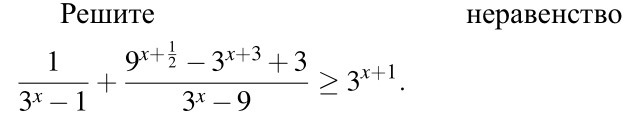
Ответы
Ответ дал:
0
Сначала нужно найти область допустимых значений - значения в знаменателе не могут быть равны нулю:
Затем необходимо привести все степенные члены к одному основанию и подставить их в неравенство:
Затем нужно произвести замену переменной (для удобства, делать это необязательно) и упростить уравнение:
Теперь производится обратная замена переменной, определятся значение x и записывается ответ с учётом ОДЗ:
Вас заинтересует
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад