Question

Найдите площадь фигуры, ограниченной линиями y=6-x, y=√x и y=0.

Answer 1

Ответ:

Пошаговое объяснение:

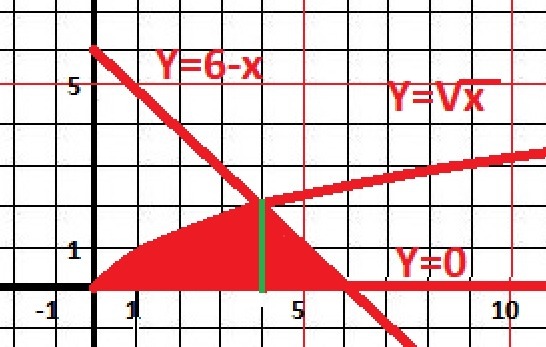
Рисунок к задаче в приложении. Два участка. От Х=0 до Х=4 функция Y = √x и  от х= 4 до х = 6 функция Y = 6-x,

Площадь - интеграл функции.

$S_{1}=intlimits^4_0 {sqrt{x} } , dx=frac{2}{3}sqrt[2]{x^3}$

$S_{2}=intlimits^6_4 {(-6+x)} , dx=frac{-6x}{1}+frac{x^2}{2}$

Вычисляем разности каждого из интегралов.

S₁ = S₁(4) - S₁(0).

S₂ = S₂(6) - S₂(4) = (-36 + 36/2) - (-24 + 16/2) = 18 - 12 = 6  

S = 7 1/3