Ответы
Ответ дал:
0
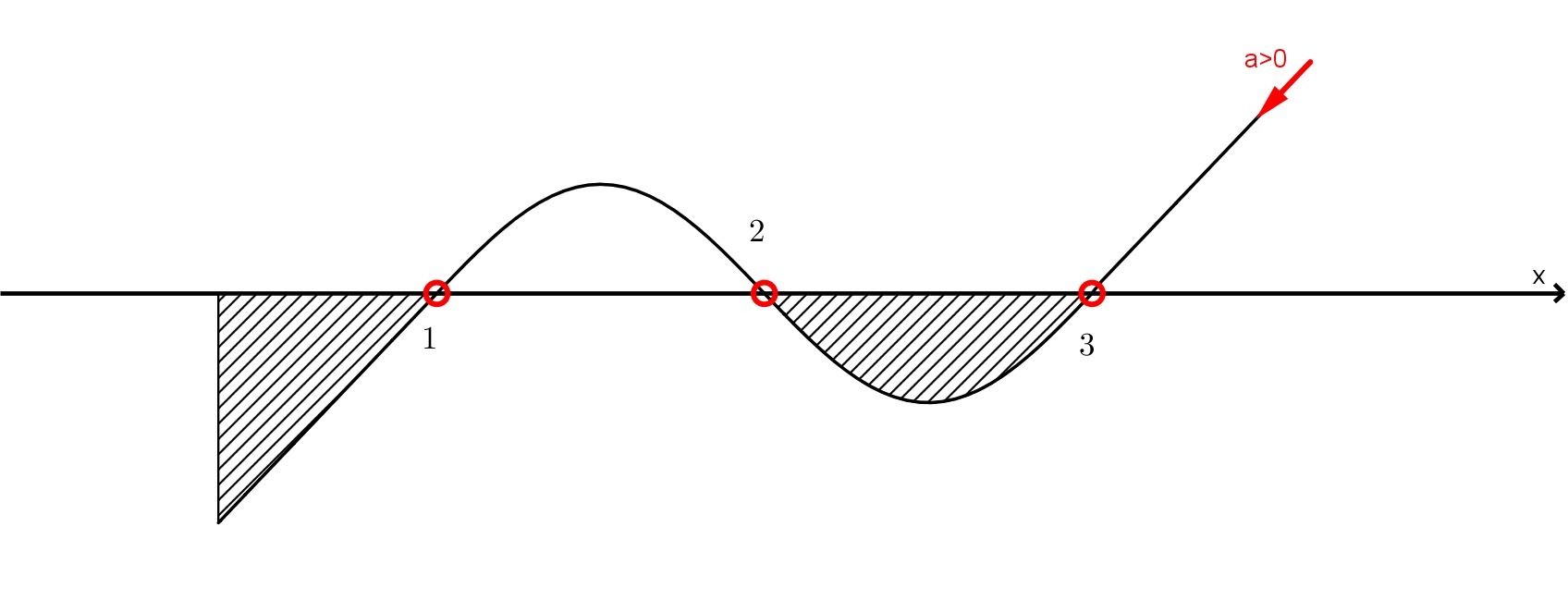
f(x)*f'(x)<0
f(x) =x^2-4x+3
Приложения:
Вас заинтересует
2 года назад
2 года назад
3 года назад
10 лет назад