Question

Геометрия, пирамиды
Задание B2

Answer 1

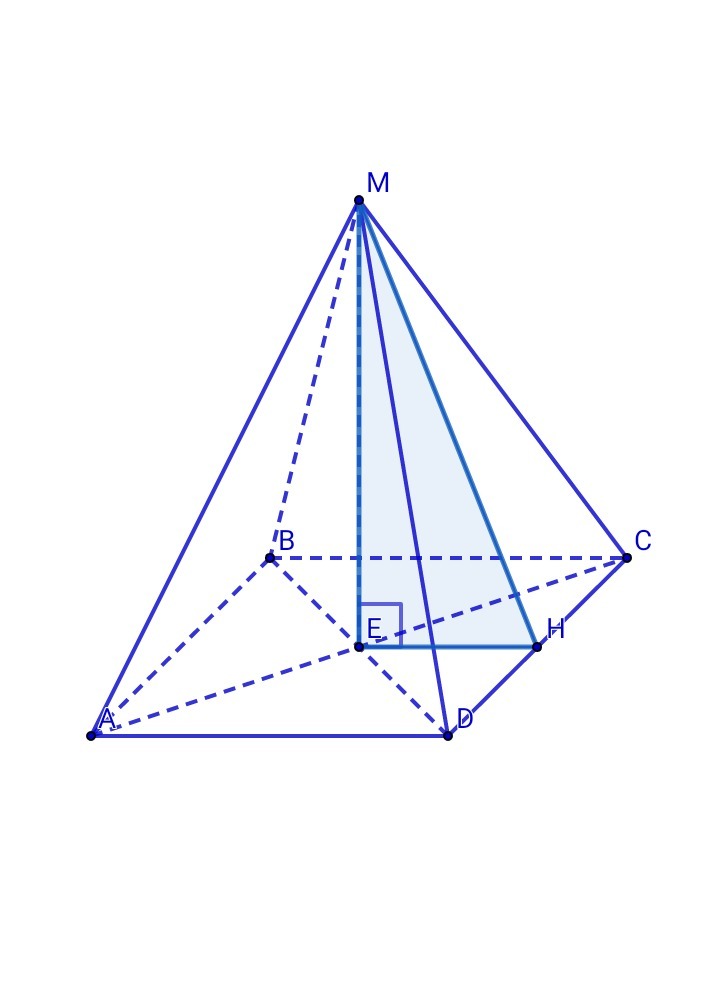
Как известно, угол между плоскостями - это линейный угол двугранного угла. Опустим перпендикуляр из точки Е на прямую CD, EH⊥CD, МЕ⊥ЕН ⇒ по теореме о 3-х перпендикулярах  МH⊥CD. Значит, ∠МHE - искомый

В ΔМЕН: tg∠MHE = ME/EH = a/(a/2) = 2  ⇒  ∠MHE = arctg(2)

Теперь перейдём ко второй цели: ориентируемся также.

Опустим из точке B и D на прямую МС перпендикуляры BK и DK, они падают на общую точку К.

AC = a√2 , AE = EC = a√2/2

В ΔМЕС: МС² = МЕ² + ЕС² = а² + (a√2/2)² = a² + (a²/2) = 3a²/2

MC = a√6/2

В ΔМЕН: МН² = МЕ² + ЕН² = а² + (а/2)² = а² + (а²/4) = 5а²/4

МН = а√5/2

B ΔCDM: S = (1/2)•CD•MH = (1=2)•MC•DK

DK = CD•MH/MC = a•(a√5/2) / (a√6/2) = a√30/6

BK = DK = a√30/6

В ΔBDK: по т. косинусов

BD² = BK² + DK² - 2•BK•DK•cos∠BKD

2a² = (5a²/6) + (5a²/6) - 2•(5a²/6)•cos∠BKD

cos∠BKD = - 1/5

∠BKD = arccos(-1/5) = π - arccos(1/5)

или можно опустить высоту в ΔBDK, это будет КЕ, КЕ⊥BD.

В ΔМЕС:  если из вершины прямого угла прям. тр-ка  опустить высоту на гипотенузу, то ME•EC = MC•EK, легко доказывается через 2 площади.

ЕК = ME•EC/MC = a•(a√2/2) / (a√6/2) = a√3/3

BE = ED = BD/2 = a√2/2

В ΔKED: tg∠EKD = ED/KE = (a√2/2)/(a√3/3) = √6/2

tg(2•∠EKD) = 2•(√6/2) / ( 1 - (√6/2)² ) = √6/(-1/2) = - 2√6

2•∠ЕКD = ∠BKD = arctg(-2√6)

Это то же самое, что и угол arccos(-1/5)

Думаю, второй способ будет полегче.

ОТВЕТ: arctg(2) ; arccos(-1/5)

Answer 2

Оооооогромное спасибо ^_^