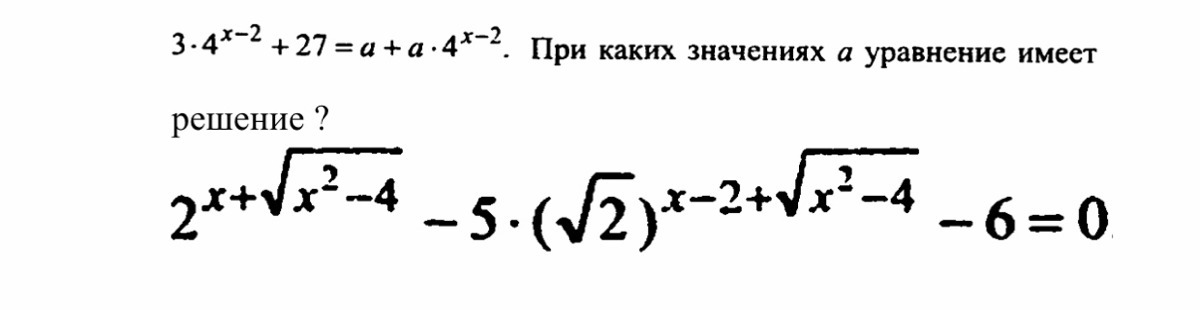Ответы
Ответ дал:
0
Под знаком логарифма должно быть положительное число:
Ответ дал:
0
Да, можно продолжать и с логарифмом. Но уже на этапе степени можно показать, что значение 4^(х-2)>0.
Ответ дал:
0
Согласен
Ответ дал:
0
Решение задания приложено
Приложения:
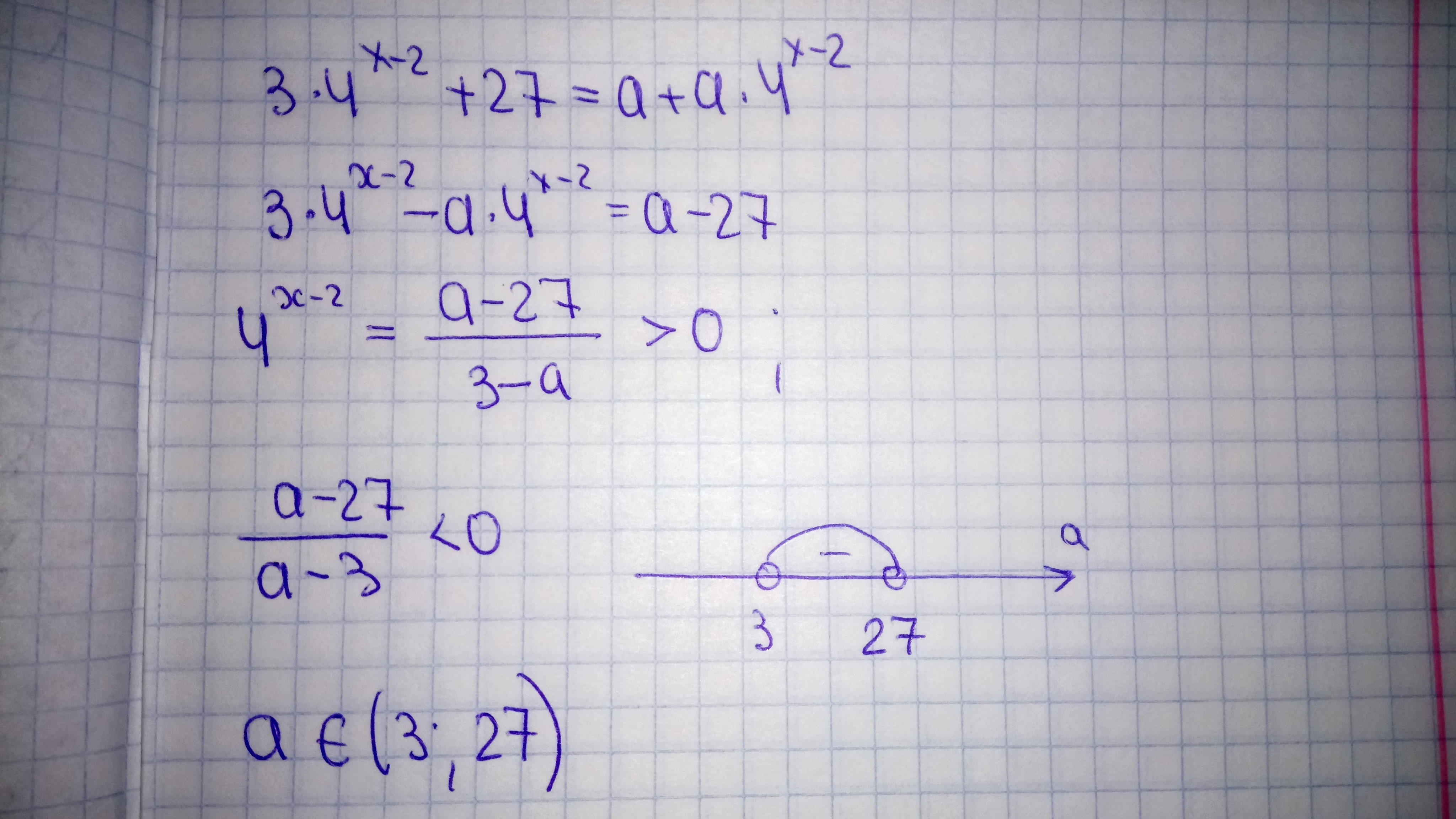

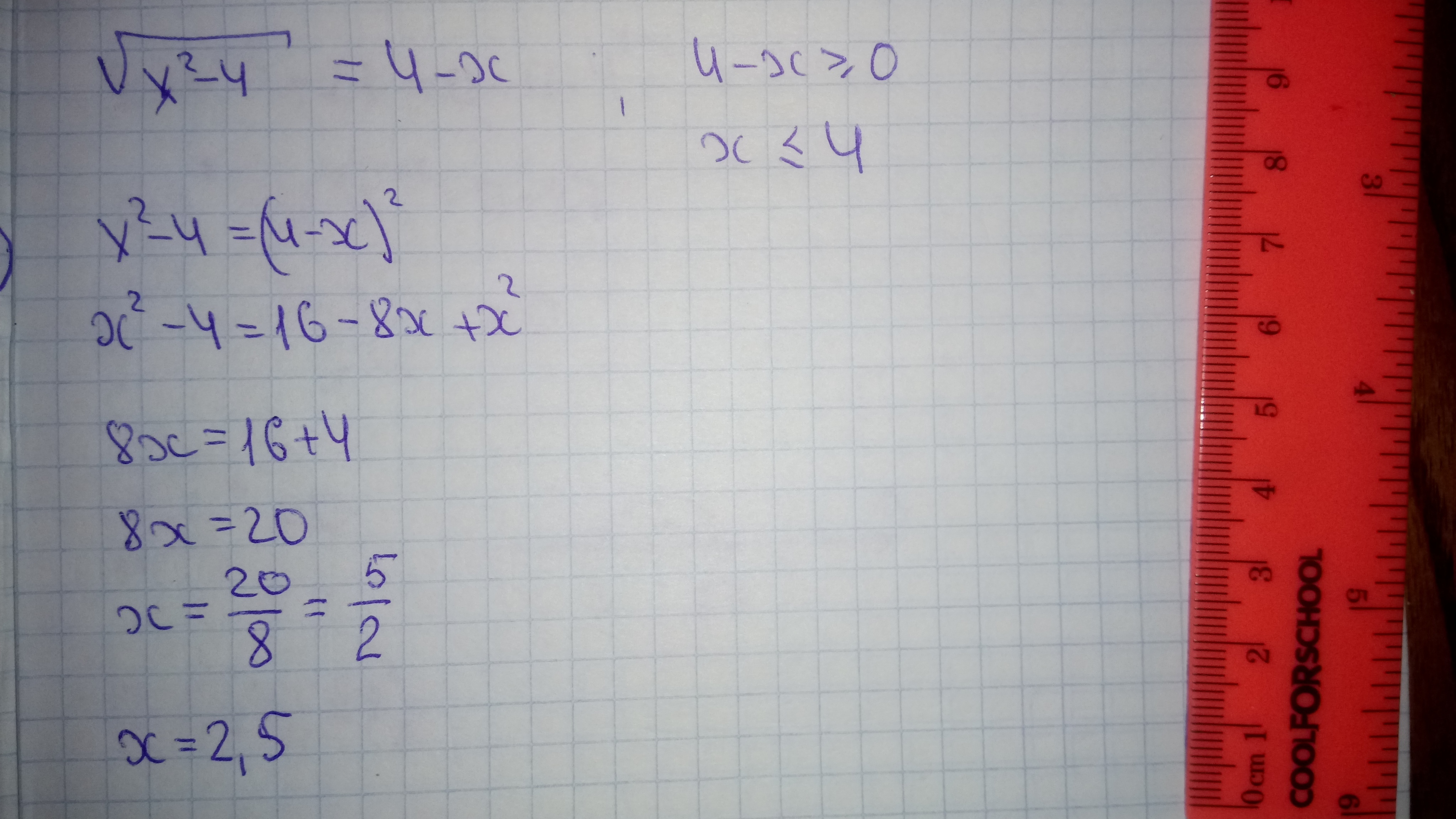
Вас заинтересует
2 года назад
2 года назад
3 года назад
9 лет назад