Вычислить значения частных производных f’x (M0), f’y (M0), f’z (M0) для данной функции f (x,y,z) в точке M0 (x0,y0,z0) с точностью до двух знаков после запятой.
Приложения:
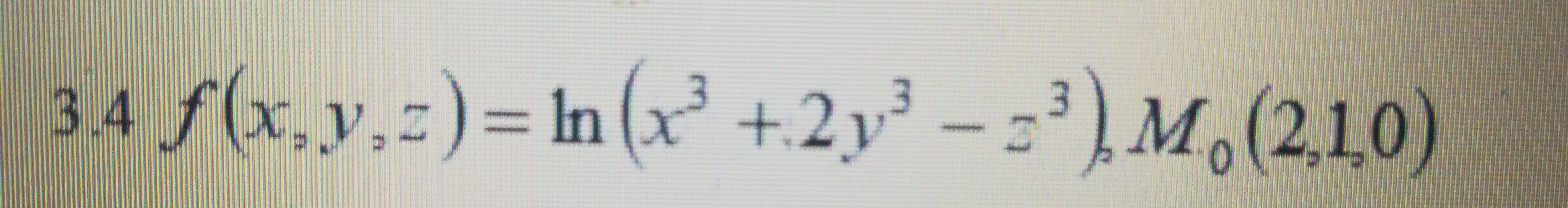
Ответы
Ответ дал:
0
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад