в равнобедренной трапеции диагональ перпендикулярна боковой стороне. Найдите площадь трапеции, если большее основание = 8 корень из 3 , а один из углов трапеции равен 60 градусов
Ответы
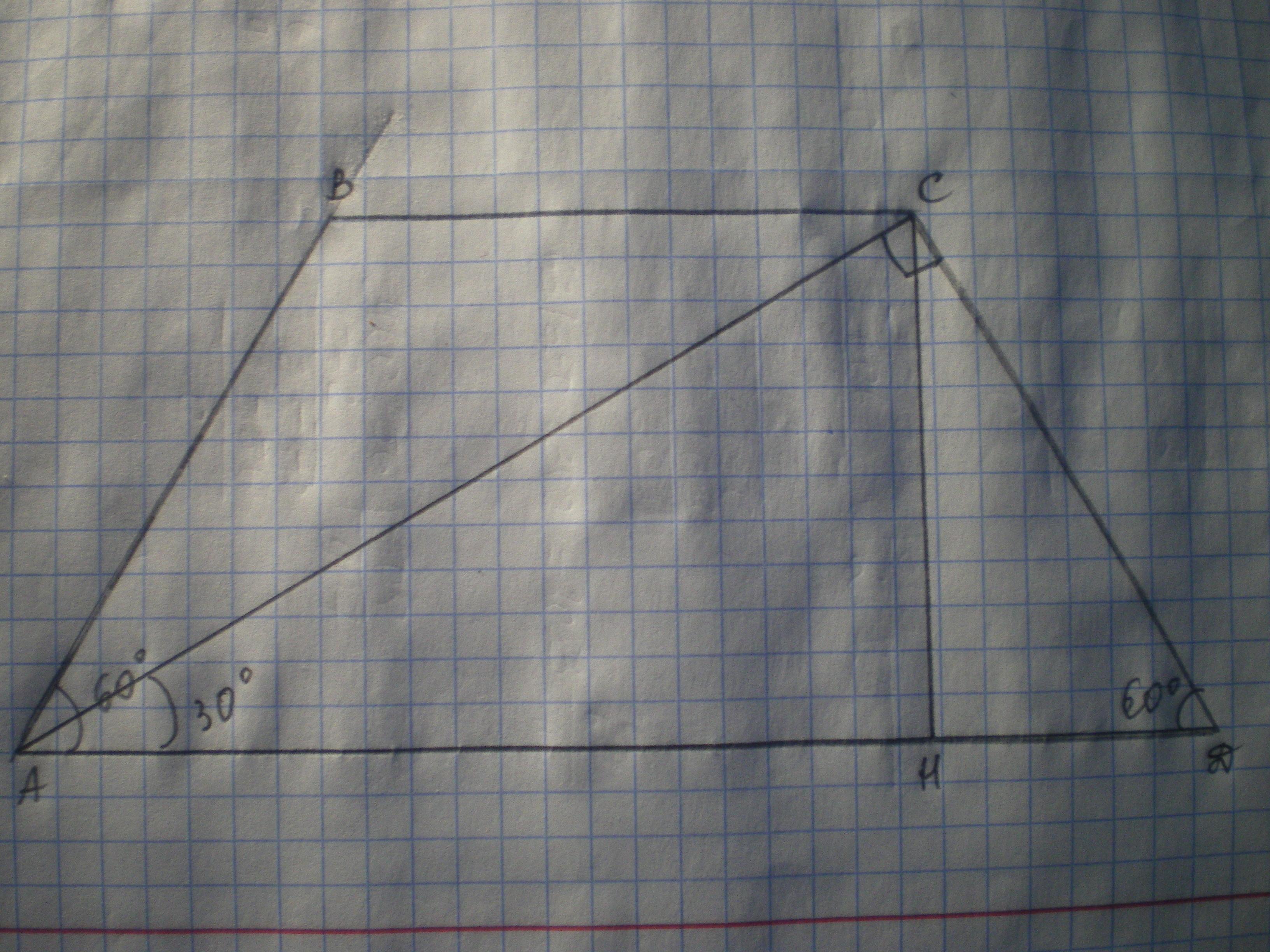
Дано: АВСД - трапеция, АВ=СД, АД=8√3, ∠А=∠Д=60°, АС⊥СД. Найти S(АВСД).
Решение: Проведем высоту СН, тогда S(АВСД)=(ВС+АД):2*СН.
Рассмотрим ΔАСД - прямоугольный, ∠Д=60°, тогда ∠САД=90-60=30°, а СД=12 АД=8√3:2=4√3.
Диагональ АС перпендикулярна к боковой стороне и делит угол А пополам, значит большее основание трапеции в два раза больше меньшего основания и её боковых сторон; и высота трапеции равна половине её диагонали.
СД=ВС=8√3:2=4√3;
АС²=(8√3)²-(4√3)²=192-48=144; АС=√144=12.
СН=12 АС=12:2=6.
S(АВСД)=(4√3+8√3):2*6=36√3 (ед²).
Ответ: 36√3 ед²
АВ=8√3/2=4√3 - катет прямоугольного треугольника лежащий против угла 30°.Тогда площадь треугольника АВД: 8√3*4√3*sin60°/2=24√3 ед².
Треугольник ВСД равнобедренный (угол В=углу Д) ⇒ВС=СД=4√3. Тогда площадь треугольника ВСД: 4√3*4√3*sin120°/2=12√3 ед². Площадь трапеции - сумма площадей треугольников:
24√3+12√3=36√3 ед².
