Question

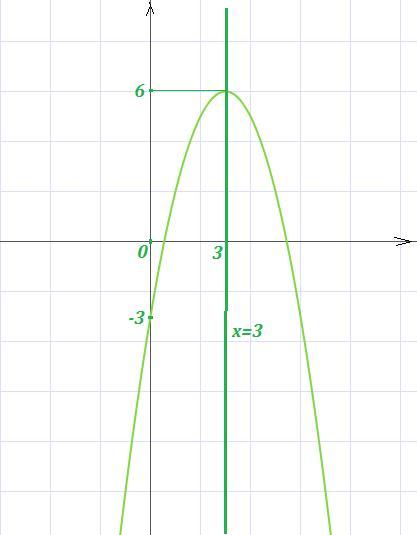
для графика квадратичной функций y=-x^2+6x-3 найдите
1)ось симметрий
2)промежуток возрастания ,убывания
3)наибольшие значение функций
4)множество значений функций
5) Расстояние от вершины параболы до начальной координаты
По возможности распишите пожалуйста

Answer 1

$y=-x^2+6x-3$

1) Ось симметрии проходит через вершину параболы, параллельно оси ОУ. Абсцисса вершины равна  $x=-frac{b}{2a}=-frac{6}{-2}=3$  .

Уравнение оси симметрии:  $x=3$  .

2)  Так как ветви параболы направлены вниз (а=-1<0), то промежуток возрастания  $(-infty ,3)$  , а промежуток убывания  $(3,+infty )$ .

3) Наибольшее значение функция принимает в своей вершине:

$y(3)=-3^2+6cdot 3-3=-9+18-3=6$

4)  Множество значений функции:  $yin (-infty ,6, ]$ .

5)  Расстояние от вершины параболы до начала координат равно

$d=sqrt{(x_1-x_2)^2+(y_1-y_2)^2}=sqrt{(3-0)^2+(6-0)^2}=sqrt{9+18}=\\=sqrt{27}=sqrt{9cdot 3}=3sqrt3$