Question

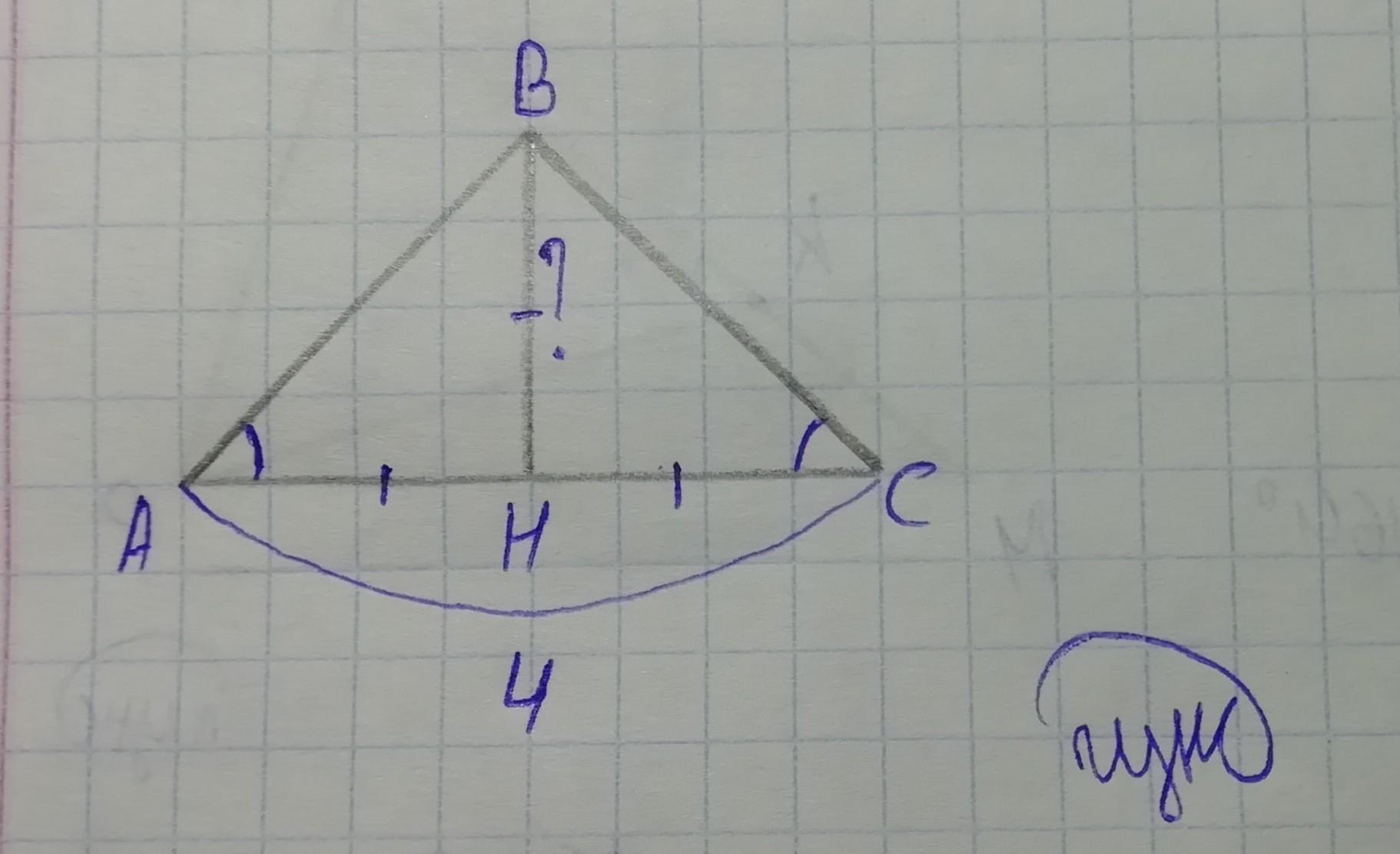
Найти расстояние от вершины равнобедренного треугольника до основания , если угол при основании в 2 раза меньше угла при вершине, а основание 4 см.
Помогите, прошу((​

Answer 1

В равнобедренном треугольнике углы при основании равны.

Пусть x - угол при основании (∠A и ∠C), тогда угол при вершине (∠B) равен 2x. Получим уравнение

x + x + 2x = 180 (сумма углов треугольника равна 180°)

4x = 180

x = 180/4 = 45°

AH = AC/2 = 4/2 = 2 см (расстояние есть высота, а высота в равнобедренном треугольнике, проведенная к основанию, является его медианой, т. е. делит основание на 2 равные части)

Рассмотрим ΔABH: ∠H = 90°, ∠A = 45°

∠B = 90 - 45 = 45° (сумма острых углов прямоугольного треугольника равна 90°) ==> ΔABH - равнобедренный ==> AH = BH = 2 см

BH есть расстояние от вершины равнобедренного треугольника до основания.

Ответ: BH = 2 см

Answer 2

спасибо, огромное, выручаете!))