Question

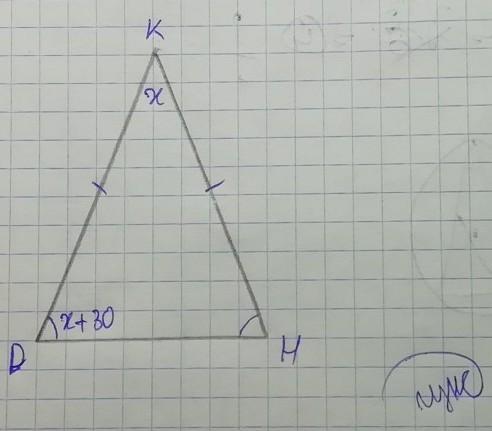
в равнобедренном треугольнике kdh с основанием dh угол kdh на 30 больше угла dkh. Найдите углы треугольника

Answer 1

x это dkh, a остальные два угла это х+30;

х+30+х+30+х=180;

3х=180-60=120, х=40
kdh=40+30=70,
khd=70,
dkh=40

Answer 2

спасибо

Answer 3

Треугольник называется равнобедренным, если его две стороны равны.

Пусть x° - ∠DKH, тогда ∠KDH = ∠DHK = x + 30°. Получим уравнение

x + x + 30 + x + 30 = 180 (сумма углов треугольника равна 180°)

3x + 60 = 180

3x = 180 - 60

3x = 120

x = 120/3 = 40° - ∠DKH

1)  ∠KDH = ∠DHK = x + 30° = 40 + 30 = 70°

Ответ: ∠DKH = 40°, ∠KDH = ∠DHK = 70°

Answer 4

спасибо