Ответы
Ответ дал:
0
1. Область определения: На ноль делить нельзя --> и х не отрицательный т.к. х под натуральным логарифмом. Итоге: x∈[0;1)∪(1;+∞)
2. Функция общего вида т.к. f(-x)≠±f(x)
3. Точки пересечения с осями:
Только одна точка (0;0)
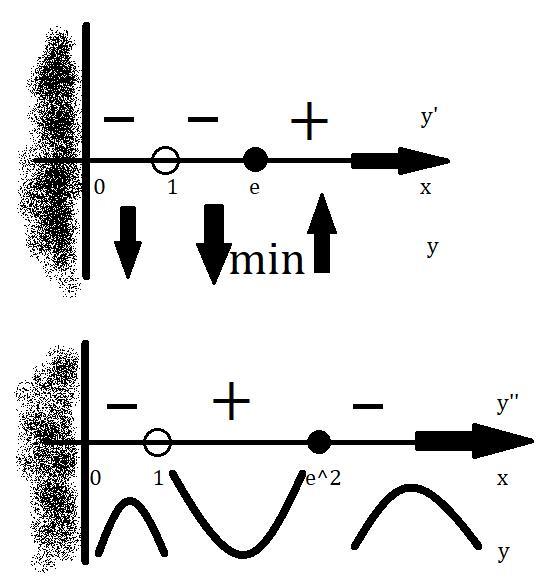
4. Исследование с 1ой производной:
см. внизу.
5. Исследование со 2ой производной:
см. внизу.
6. Асимптоты:
Уравнения наклонных асимптот обычно ищут в виде y = kx + b. По определению асимптоты:
Находим коэффициент k:
Находим коэффициент b:
Предел равен ∞, следовательно, наклонные асимптоты функции отсутствуют.
Найдем вертикальные асимптоты. Для этого определим точки разрыва:
Находим переделы в точке 1:
Значит точка разрыва II рода и является вертикальной асимптотой.
Приложения:
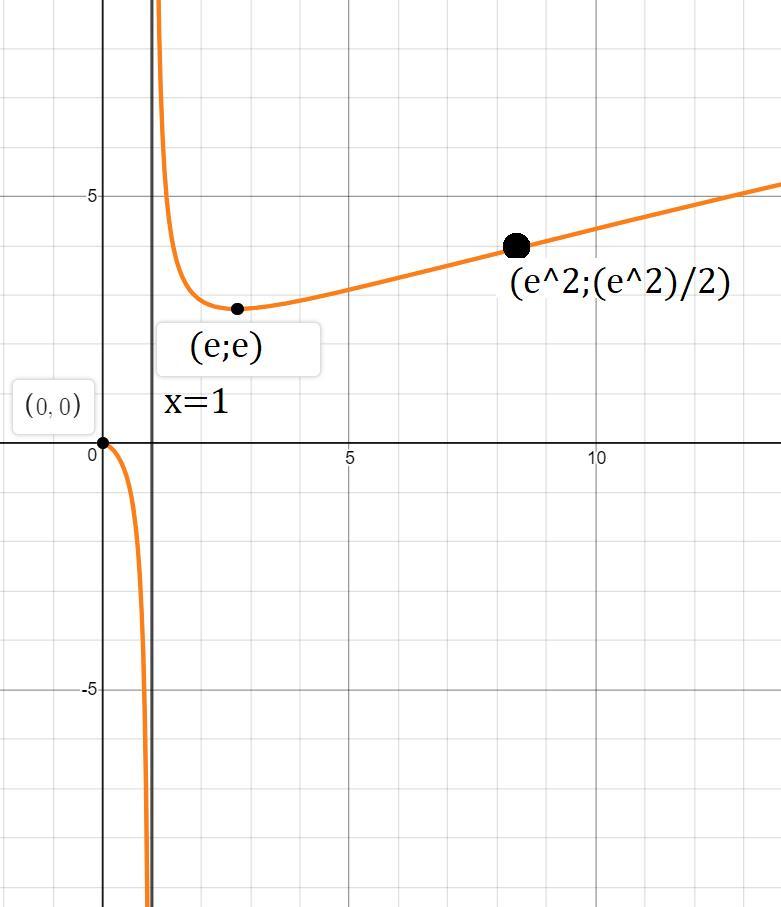
Ответ дал:
0
Спасибо большое, помогите пожалуйста с этим заданием 25 б https://znanija.com/task/32014605
Вас заинтересует
2 года назад
2 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад
