Ответы
Ответ:
Сформулируем теорему о биссектрисе угла:
Любая точка биссектрисы любого угла (кроме развернутого) является равноудаленной от сторон данного угла.
Докажем теорему.
Доказательство.
Пусть точка M является произвольной точкой биссектрисы неразвернутого угла A.
Проведем к сторонам угла А перпендикулярные прямые MF и MG.
Таким образом, мы получим два прямоугольных треугольника AMF и AMG, которые являются равными между собой по стороне (гипотенузе) и острому углу (сторона AM является общей гипотенузой, а углы равны по свойству биссектрисы согласно условию).
Значит, прямые MF = MG.
Теорема доказана.
Сформулируем также обратную теорему:
Каждая точка, которая лежит в середине неразвернутого угла и равноудалена от сторон этого угла, принадлежит его биссектрисе.
Докажем данную теорему.
Доказательство.
Возьмем точку Q, лежащую в середине неразвернутого угла С и равноудаленную от его сторон. Тогда перпендикулярные прямые QH и QK, проведенные к сторонам угла, равны.
Докажем, что прямая CQ является биссектрисой угла С.
Рассмотрим полученные прямоугольные треугольники СQH и CQK. У них сторона CQ является общей, а стороны QH и QK равны согласно условию. Таким образом, данные треугольники будут равными по катету и гипотенузе. Так как у равным треугольников и соответствующие углы также равны, то получаем, что прямая CQ действительно будет биссектрисой угла С.
Теорема доказана.
Объяснение:
Ответ:
Каждая точка биссектрисы угла равноудалена от сторон угла.
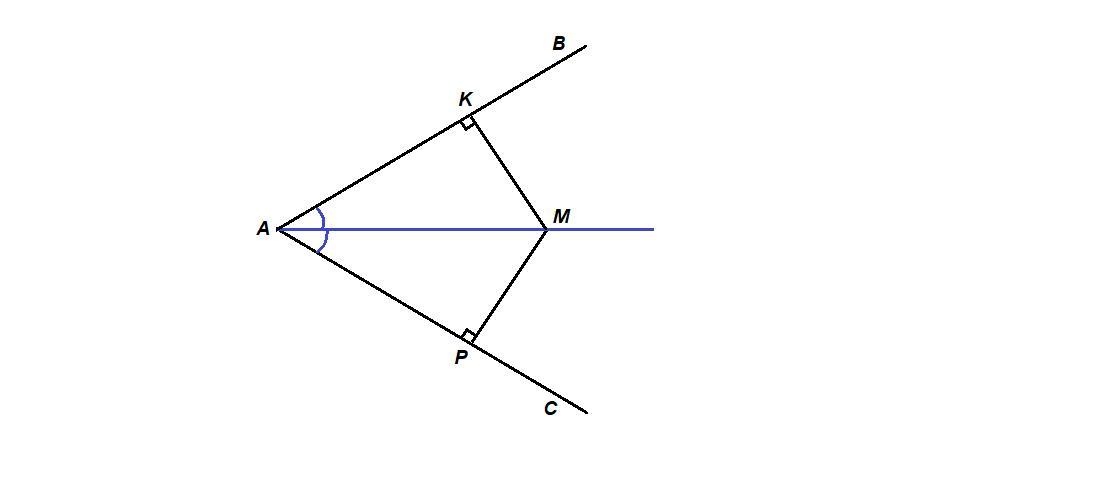
Дано: ∠ВАС, АМ - биссектриса,
Доказать: d(M, BA) = d(M, CA).
Доказательство:
Проведем МК⊥АВ и МР⊥АС.
МК - расстояние от точки М до АВ, т.е. d(M, AB) = MK,
MP - расстояние от точки М до АС, т.е. d(М, АС) = МР.
Докажем, что МК = МР.
Рассмотрим треугольники АКМ и АРМ:
∠АКМ = ∠АРМ = 90°,
∠КАМ = ∠РАМ, так как АМ - биссектриса,
АМ - общая сторона, ⇒
ΔАКМ = ΔАРМ по гипотенузе и острому углу.
Значит, МК = МР, что и требовалось доказать.