Question

Прошу пояснить условие.
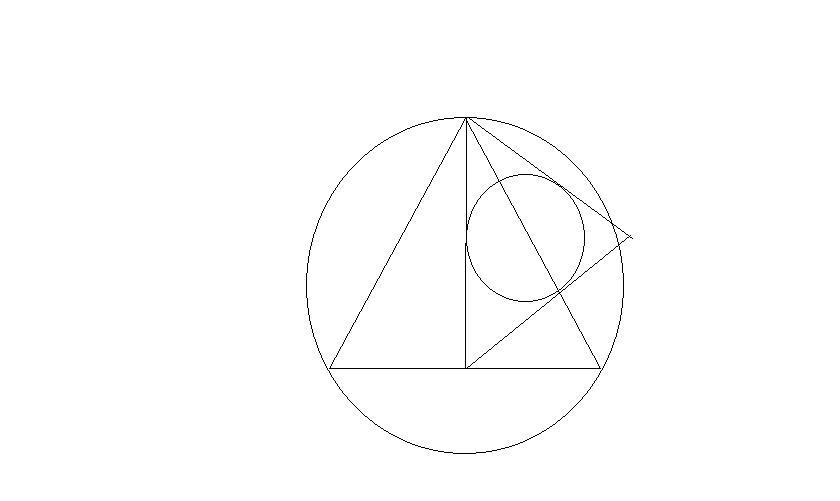
В окружность радиуса √3 вписан правильный треугольник. На его высоте как на стороне построен другой правильный треугольник, в который тоже вписана окружность. Найдите его радиус.

Answer 1

...............................................

Answer 2

Да)

Answer 3

ну расписывай!

Answer 4

пока

Answer 5

r (мал.) = 0,75

Answer 6

я не решала...

Answer 7

По заданному радиусу определяем сторону первого вписанного треугольника: a1 = 2*(R1*cos 30°) = 2*√3*(√3/2) = 3.

Высота этого треугольника (равная стороне второго треугольника) h1 = а2 = a1*cos 30° = 3*(√3/2).

Радиус вписанной окружности во второй треугольник равен:

r2 = (a2/2)*tg 30° = 3*(√3/4)*(1/√3) = 3/4 = 0,75.