Question

ПОМОГИТЕ ПОЖАЛУЙСТА!!

Answer 1

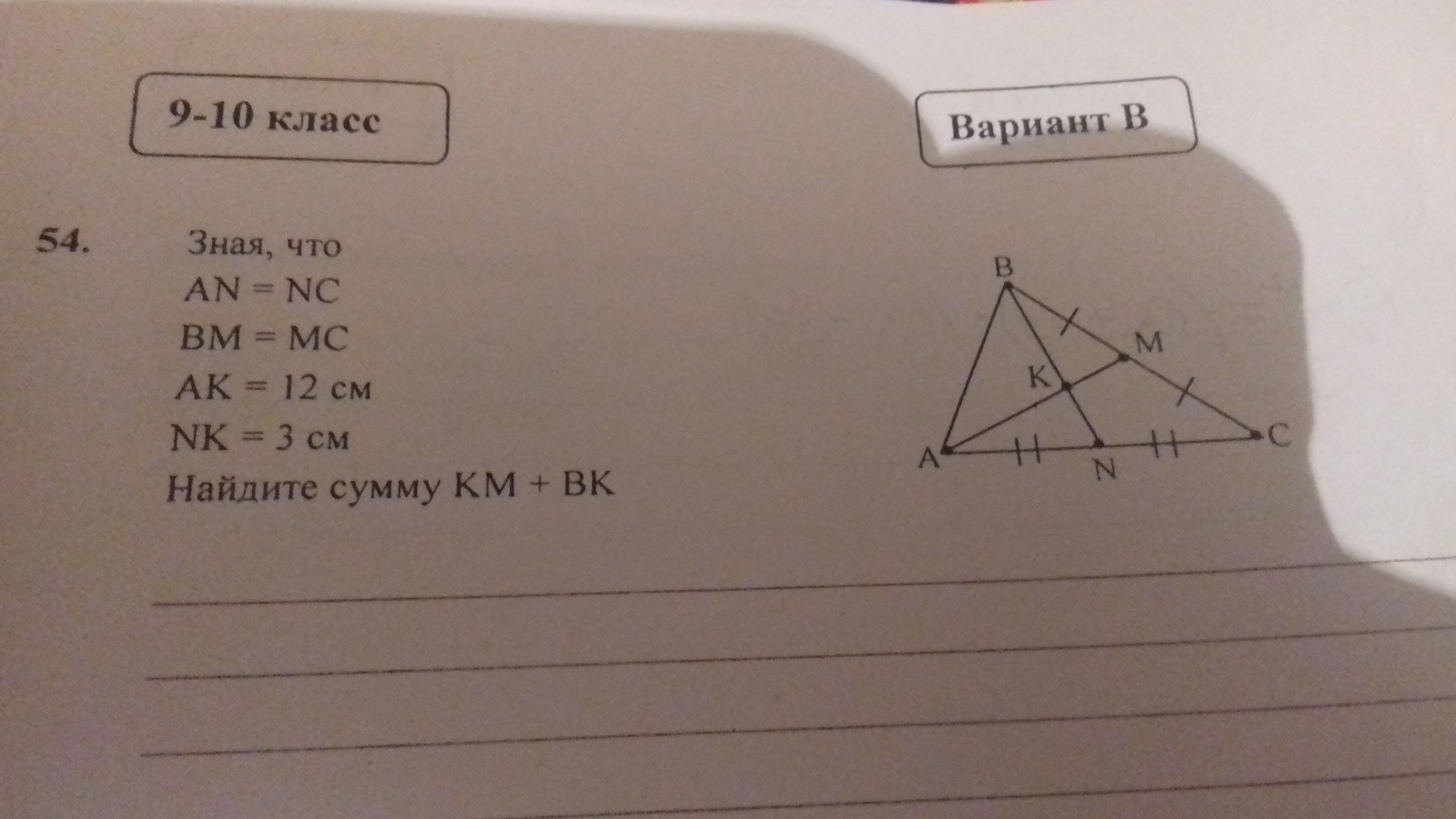
Т.к. по условию СМ=МВ, АN=NC, то BN и АМ являются медианами треугольника АВС.

Свойство медиан. Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины.

По свойству медиан:
1) BK:KN=2:1; ВК:3=2:1; ВК=6 см
2) АК:КМ=2:1; 12:КМ=2:1; КМ=6 см

Таким образом, КМ+ВК=6+6=12 см.

Ответ: 12 см.

Answer 2

Ответ:

Объяснение:

Медианы треугольника пересекаются в одной точке - центре тяжести треугольника и делятся этой точкой в отношении 2 : 1, считается от вершины угла:

AK:KM=2:1   KM= AK:2   KM=12:2=6см   KM+ BK=6 +6 =12см

BK:KN=2:1    BK=2*KN    BK=2*3=6см