Question

В равнобедренном треугольнике АВС с основанием АС угол В равен 120°. Высота треугольника, проведённая из вершины А, равна 5. Найдите длину стороны АС.
Помогите пожалуйста!​

Answer 1

1) <A+<B+<C=180

<С=(180-120):2

<С=30

2) рассмотрим треугольник AA1C - прямоугольный, т.к. AA1-высота, <AA1C=90

<С=30, значит

AA1=1/2AC, т.к. напротив угла в 30 градусов лежит катет, равный половине гипотенузы.

AC=2*AA1

AC=10

Ответ: 10

Answer 2

спасибо вам большое!

Answer 3

прошу прощения, у меня в 1) опечатка. там нужно рассчитать угол <С, а не B.

Answer 4

Ничего, спасибо

Answer 5

не за что, если возникают вопросы по поводу моего решения, то с радостью отвечу. :)

Answer 6

❤❤❤)

Answer 7

Ответ:

10 ед. изм.

Объяснение:

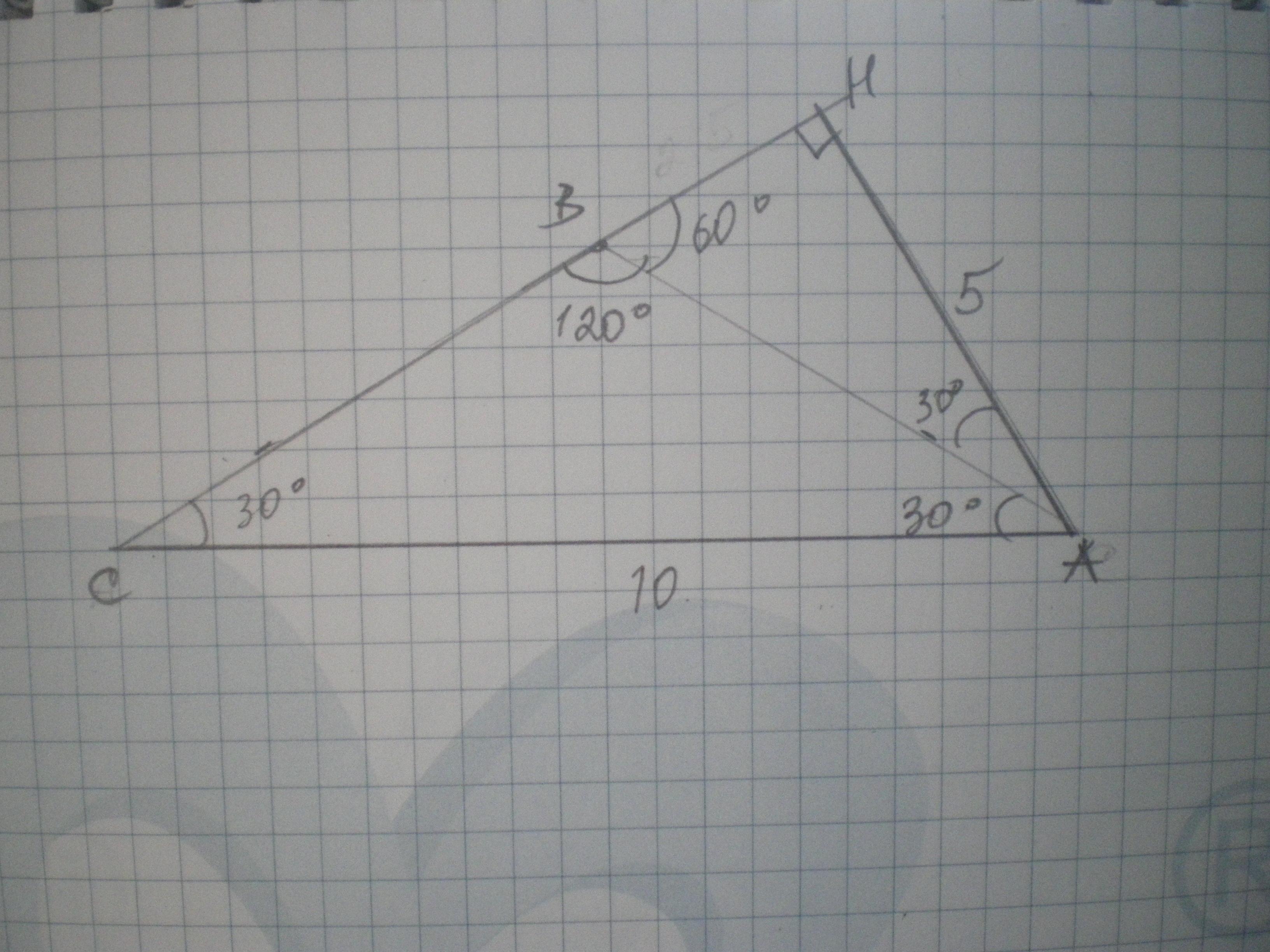
Дано: ΔАВС - равнобедренный, АВ=ВС, ∠В=120°, АН=5. Найти АС.

В тупоугольном треугольнике высота падает на продолжение противоположной стороны.

∠ВАС=∠С=(180-120):2=30°

В ΔАВН - прямоугольном ∠АВН=180-120=60°, тогда ∠ВАН=90-60=30°.

∠А=30+30=60°

В ΔАСН - прямоугольном ∠С=30°, тогда АС=2АН=5*2=10 (ед. изм.)