Ответы
Ответ дал:
0
Ответ:
Объяснение:
!!!!!!!!!!!!!!!!!!!!!!!!!!
Приложения:
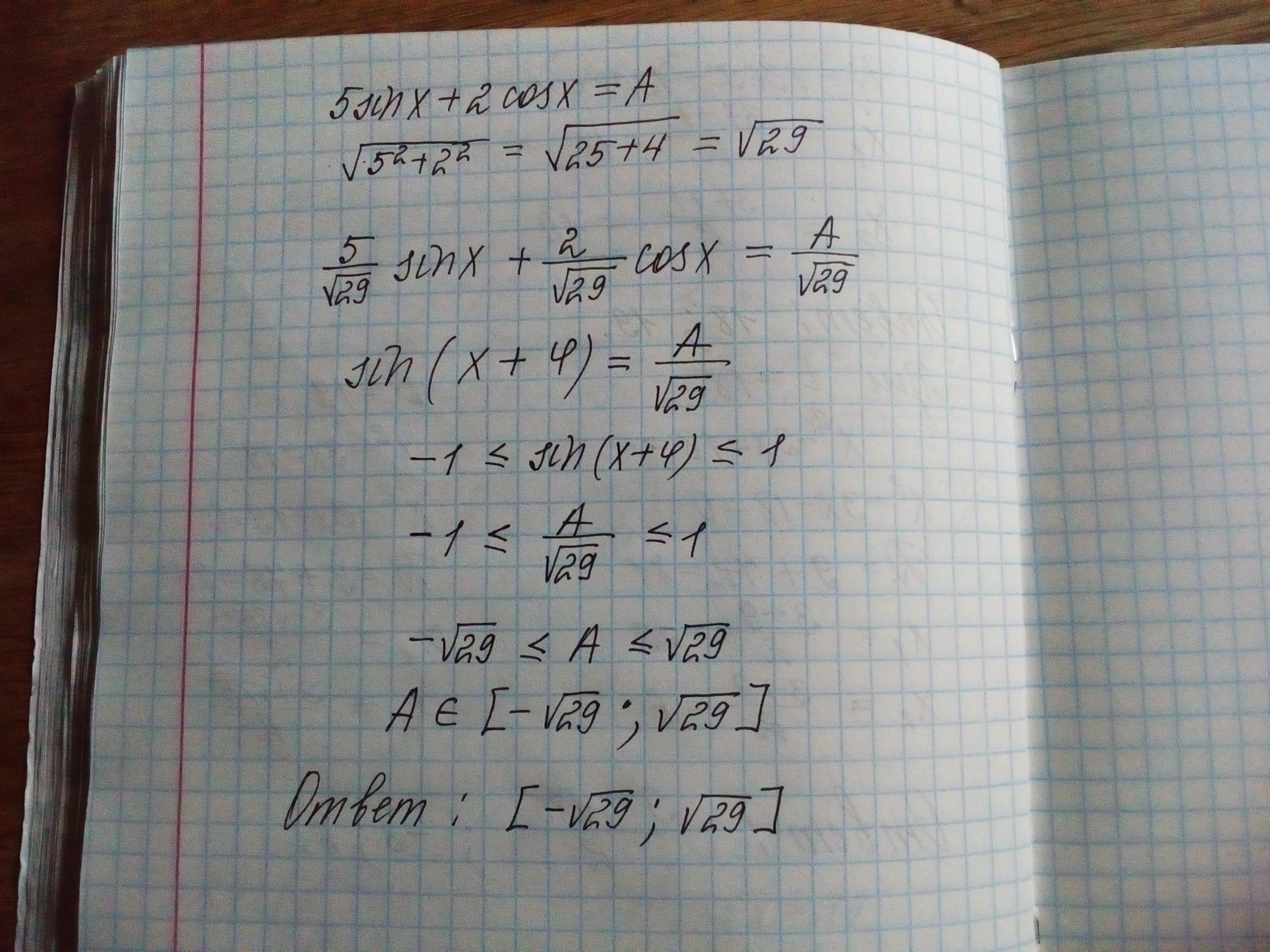
Ответ дал:
0
Ответ:
[-√29; √29]
Объяснение:
Воспользуемся формулами двойного угла.
5sin x + 2cos x = A
10sin(x/2)*cos(x/2) + 2cos^2 (x/2) - 2sin^2 (x/2) = Acos^2 (x/2) + Asin^2 (x/2)
sin^2 (x/2)*(-2 - A) + 10sin(x/2)*cos(x/2) + cos^2 (x/2)*(2 - A) = 0
Делим все на cos^2 (x/2)
tg^2 (x/2)*(-2 - A) + 10tg(x/2) + (2 - A) = 0
Получили квадратное уравнение относительно tg(x/2)
D = 100 - 4(-2-A)(2-A) = 100 + 4(4 - A^2)
Решения будут, если D >= 0
100 + 16 - 4A^2 >= 0
A^2 <= 29
A € [-√29; √29]
Приложения:
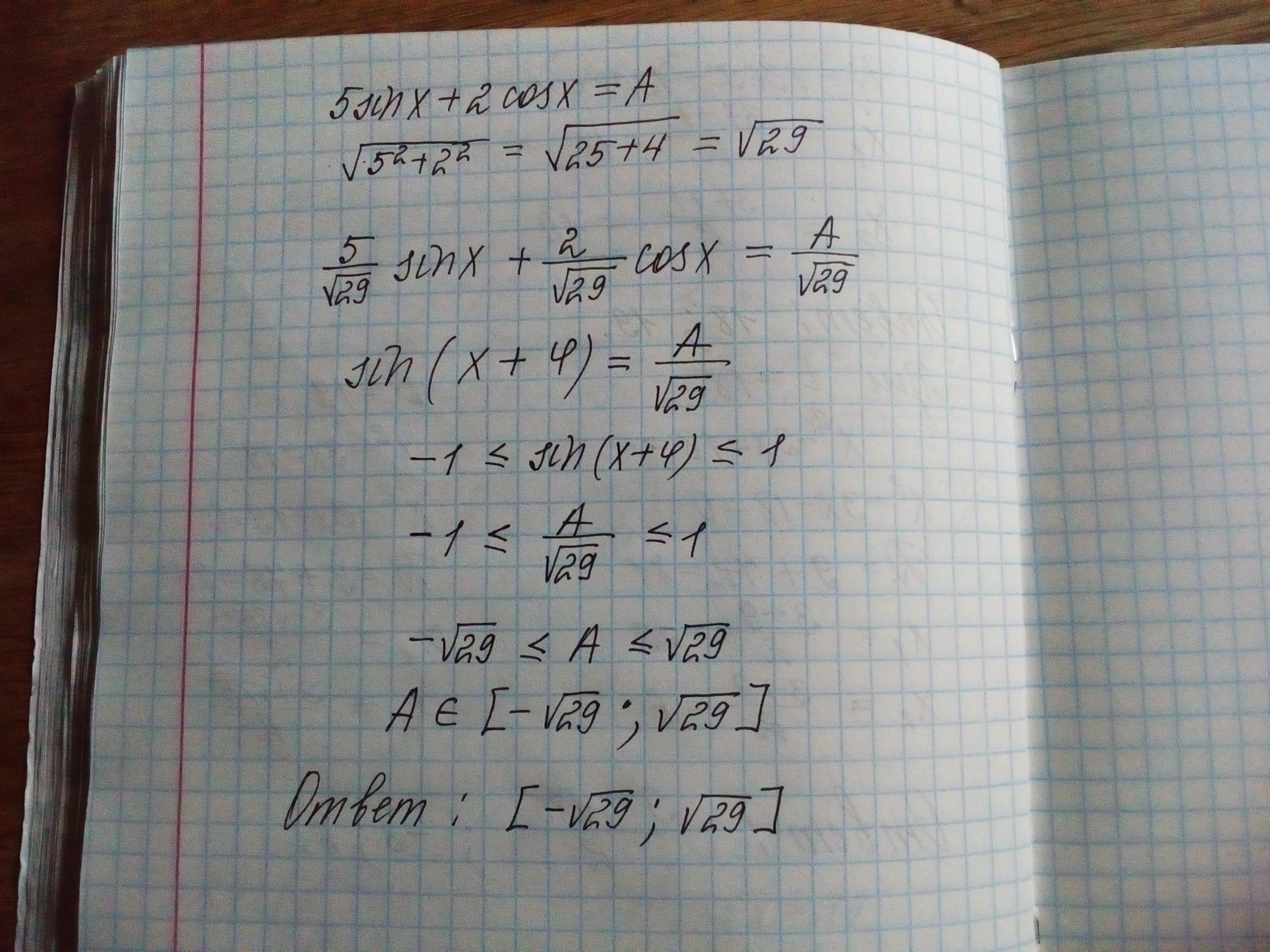
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад
10 лет назад