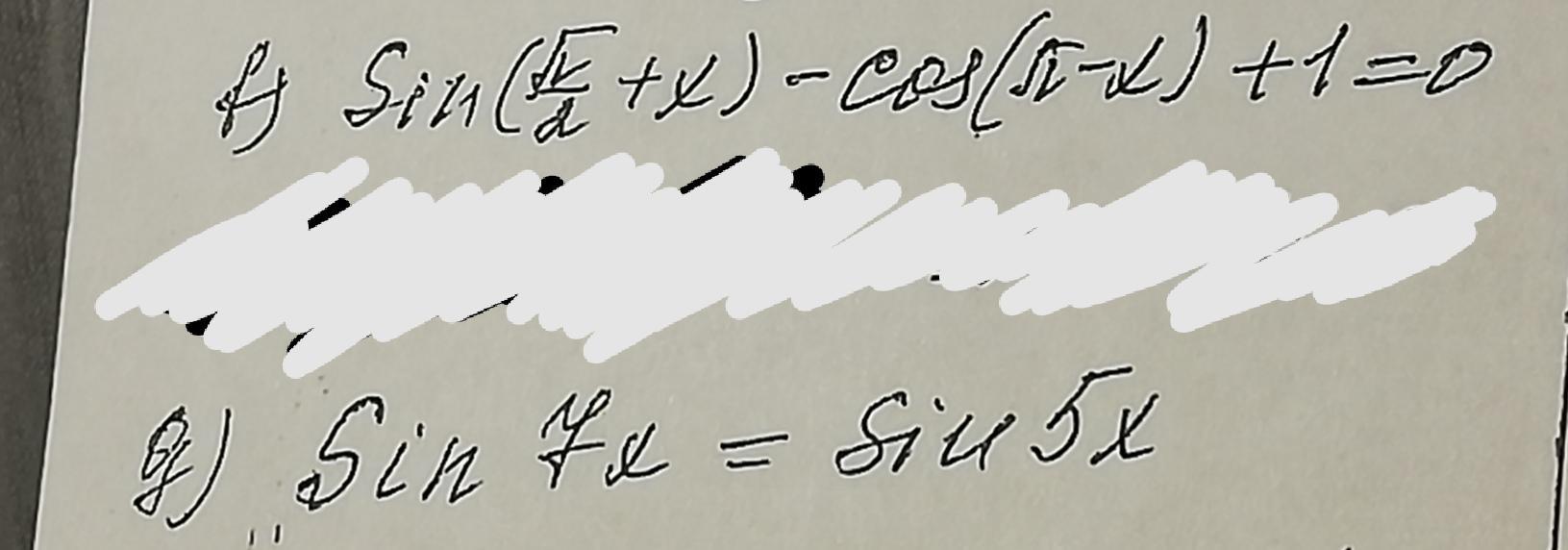Question

Решите уравнения. Пожалуйста!

Answer 1

Sin(π/2 + x) - Cos(π - x) + 1 = 0

Sin(a+b) = Sina*Cosb + Cosa*Sinb

Cos(a-b) = Cosa*Cosb + Sina*Sinb

1)Sin(π/2 + x) = Sin(π/2)*Cosx + Cos(π/2)*Sinx = Cosx

 Cos(π - x) = Cosπ*Cosx + Sinπ*Sinx = -Cosx

 Cosx - (-Cosx) + 1 = 0

 2Cosx + 1 = 0

 Cosx = -1/2

 x = ±2π/3 + 2πn, n∈Z

Sina - Sinb = 2Sin((a-b)/2)*Cos((a+b)/2)

2) Sin(7x) = Sin(5x)

   Sin(7x) - Sin(5x) = 0

   2Sinx *Cos(6x) = 0

   Sinx = 0 => x = πn, n∈Z

   Cos(6x) = 0 => 6x = π/2 + 2πn, n∈Z

                              x = π/12 + πn/3, n∈Z

   

   

Answer 2

Спасибо большое

Answer 3

Во втором уравнении частный случай косинуса не совсем верный

Answer 4

Первое некрасиво решено, во втором ошибки.

Answer 5

$Sin(frac{pi }{2}+x)-Cos(pi-x)+1=0\\Cosx+Cosx+1=0\\2Cosx=-1\\Cosx=-frac{1}{2}\\x=pm arcCos(-frac{1}{2})+2pi n,nin z\\x=pm frac{2pi }{3}+2pi n,nin z$

$Sin7x=Sin5x\\Sin7x - Sin5x=0\\2Sinfrac{7x-5x}{2}Cosfrac{7x+5x}{2}=0\\2SinxCos6x=0\\1)Sinx=0\\x=pi n,nin z\\2)Cos6x=0\\6x=frac{pi }{2}+pi n,nin z\\x=frac{pi }{12}+frac{pi n }{6},nin z$

Answer 6

Все отлично, в первом уравнении - 1 должен бвть