Ответы
Ответ дал:
0
Ответ:
Объяснение:
ВОТ
Приложения:
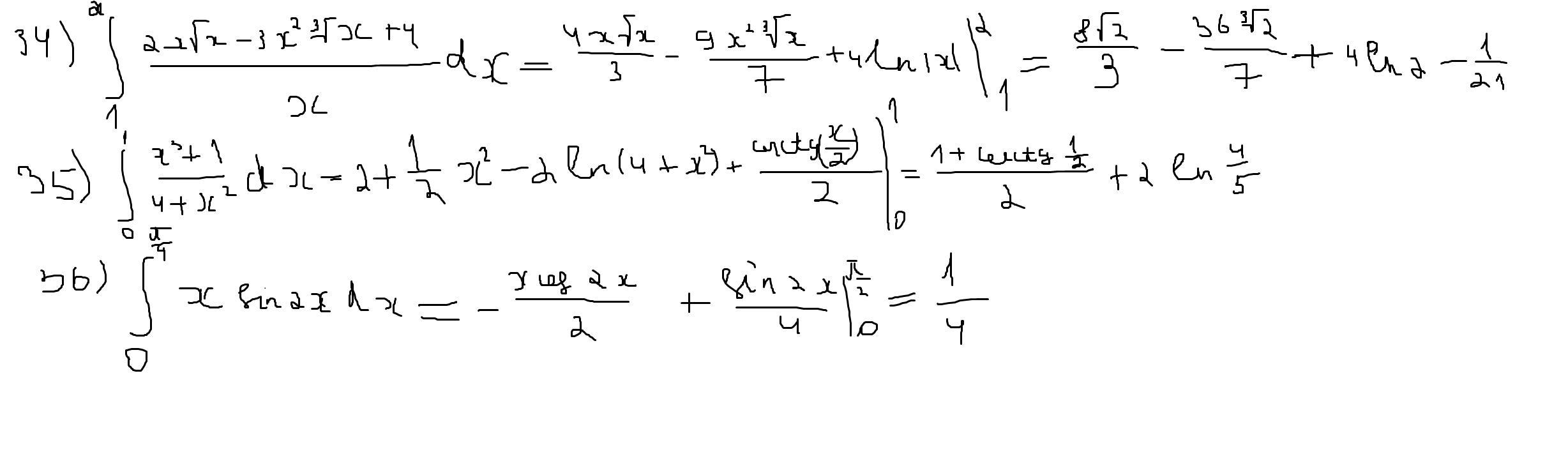
Ответ дал:
0
36. Интегрируем по частям. х=u; дх=дu; sin2xдх= дv⇒v=-cos2x/2
По формуле интегрирования по частям интеграл равен -х*cos2x/2+∫cos2xдх/2=х*сos2x/2+sin2x/4, после подстановки пределов интегрирования получим -(((π/4)*cosπ/2)/2)+((sinπ/2)/4)-(-0+0)=1/4
34.разделим на х, получим 4х√х/3-9х²∛х/7+4㏑по модулю х, подставим пределы интегрирования, получим 8√2/3-36∛2/7+4㏑2-1/21
35. интеграл равен х²/2-2㏑(х²+4)+0.5(arctg(х/2), после подстановки пределов интегрирования получим 0.5+0.5(arctg(1/2)+2㏑0.8
37. введем замену у=√х, тогда ду=дх/√х, 2∫уду/(у+1)=2у-2㏑(у+1, т.к. у/(у+1)=1-(1/(у+1)))и после подстановки вместо у получим ответ 2√х-2㏑(√х+1) после подстановки пределов
-2㏑(√3+1))+2㏑(√2+1)+2√3-2√2
Приложения:
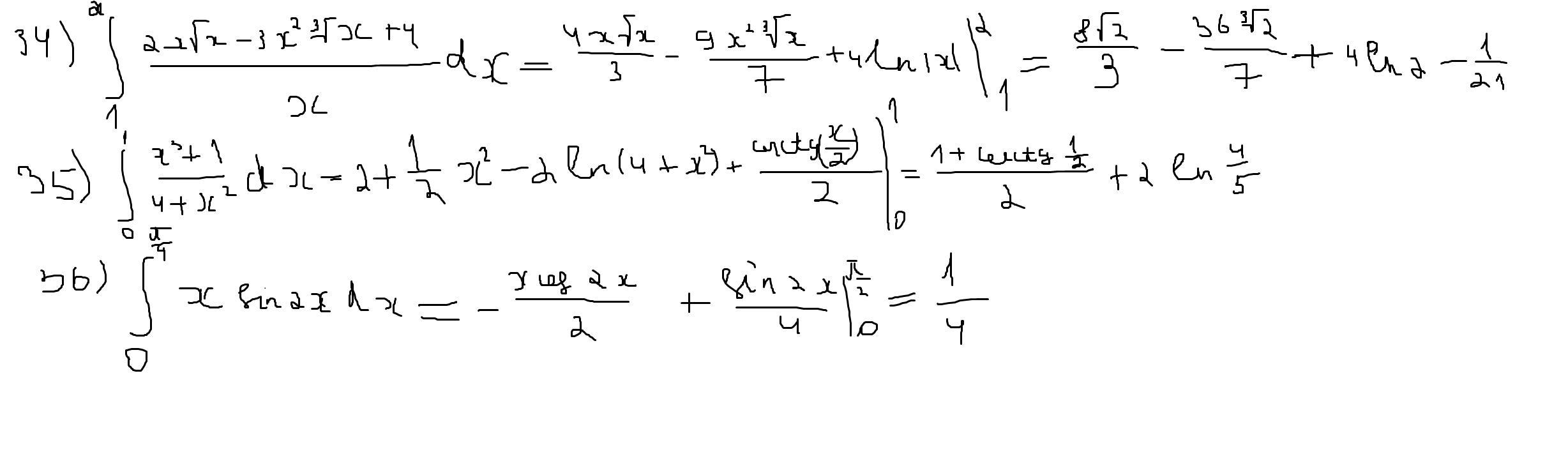
Вас заинтересует
2 года назад
2 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад
