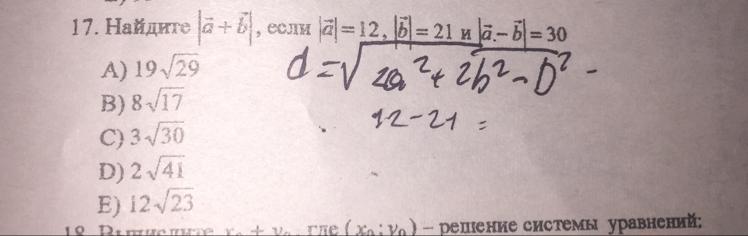Question

Помогите решить , задание во вложении

Answer 1

Смотри вниз.

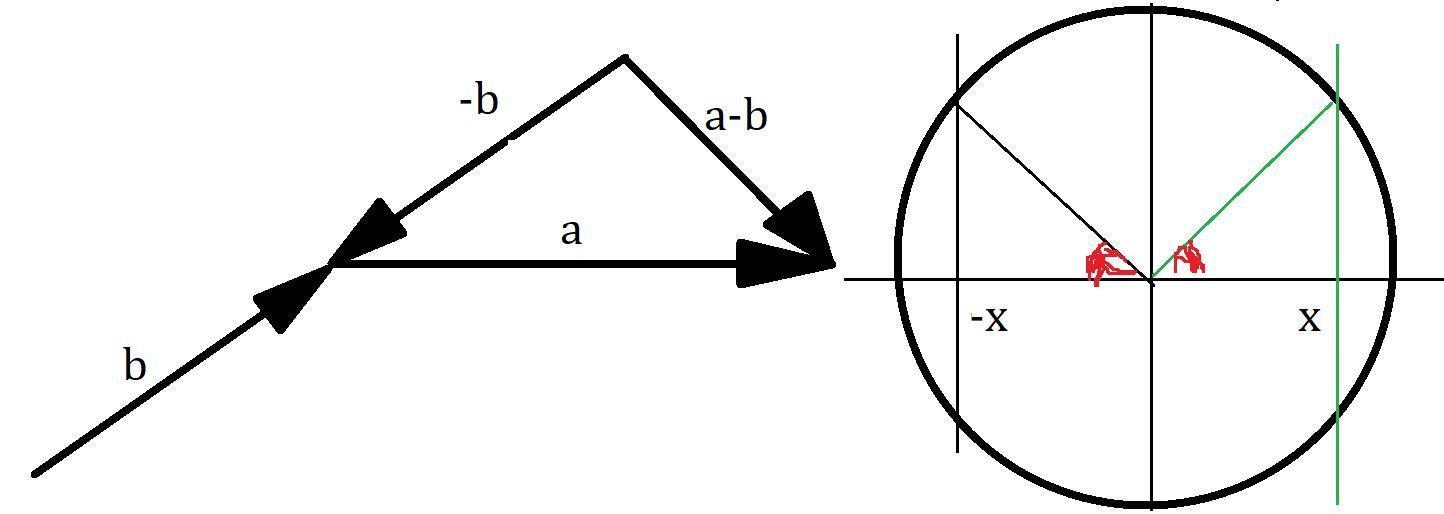
По теореме косинусов найдём угол между векторами a и (-b):

$|a-b|^2=|a|^2+|-b|^2-2|a|*|-b|cos{alpha}\cos{alpha}=frac{144+441-900}{2*12*21}=frac{-315}{2*12*21}=-x$

Если, что модуль отрицательного вектора и положительного одинаковый т.к. это его длина.

Посмотрев на картинку, можно понять, что угол между векторами a  и b равен 180° - угол между векторами a и (-b), используя тригонометрический круг, определим косинус угла между векторами a и b, смотри вниз.

Теперь найдём модуль вектора суммы.

$|a+b|=sqrt{|a|^2+|b|^2-2*|a|*|b|*frac{315}{2*12*21}}=\sqrt{144+441-315}=sqrt{270}=3sqrt{30}\Otvet:C).$