Пожалуйста, решите с пояснениями (для человека, весьма слабо разбирающегося в логарифмах)
Приложения:
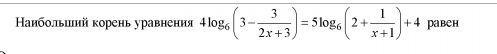
Ответы
Ответ дал:
0
ОДЗ:
Метод интервалов:
__+__ (-3/2) ___ (-1) __+___
x∈(-∞;-3/2) U (-1;+∞)
Свойства логарифма.
Логарифм степени
n·log_(6)b=log_(6)bⁿ
b>0
Логарифм произведения
log_(6) a + log_(6)b=log_(6)a·b
a>0; b>0
Уравнение принимает вид:
log₆(6(x+1)/(2x+3))⁴=log₆((2x+3)/(x+1))⁵·6⁴
Логарифмы равны, значит и выражения под логарифмами равны.
(6(x+1)/(2x+3))⁴=((2x+3)/(x+1))⁵·6⁴
Сокращаем на 6⁴
(х+1)⁴/(2х+3)⁴=(2х+3)⁵/(х+1)⁵
((x+1)/(2x+3))⁹=1
(x+1)/(2x+3)=1
x+1=2x+3
x=-2∈(-∞;-3/2) U (-1;+∞)
О т в е т. -2
Ответ дал:
0
Большое спасибо!
Ответ дал:
0
Добрый день! Вчера не было возможности разобраться в этом, но сегодня она появилась, а у меня появился вопрос. Не могу понять, откуда взялась 6 в степени 4, если изначально была просто 4?
Ответ дал:
0
4=4*1=4*log(6)6=log(6)6^4
Ответ дал:
0
О, теперь дошло, огромное спасибо)
Вас заинтересует
2 года назад
2 года назад
3 года назад
9 лет назад
9 лет назад
9 лет назад
9 лет назад