Question

Через вершины A и B треугольника ABC проведены две параллельные прямые, а прямые l1 и l2 симметричны им относительно биссектрис соответствующих углов. Докажите, что точка пересечения прямых l1 и l2 лежит на описанной окружности треугольника ABC.

Answer 1

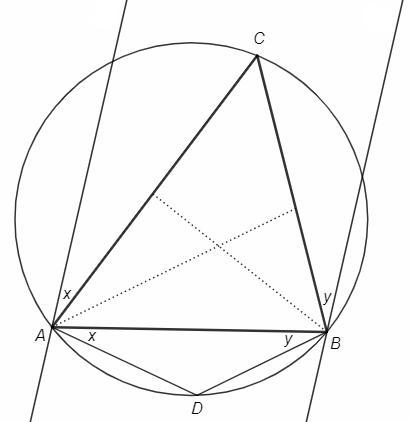
Точка D - пересечение прямых l1 и l2.

Симметричные прямые составляют равные углы с биссектрисами, а значит и со сторонами треугольника. Обозначим эти углы x и y.

Сумма внутренних односторонних углов при параллельных равна 180.

x +A +B +y =180

A +B +C =180

x +y +D =180 (△ABD)

C +D =180

ACBD - описанный четырехугольник (т.к. сумма противоположных углов равна 180), вершины лежат на одной окружности.