Question

60 баллов ☺️ Решите 11.20, пожалуйста)

Answer 1

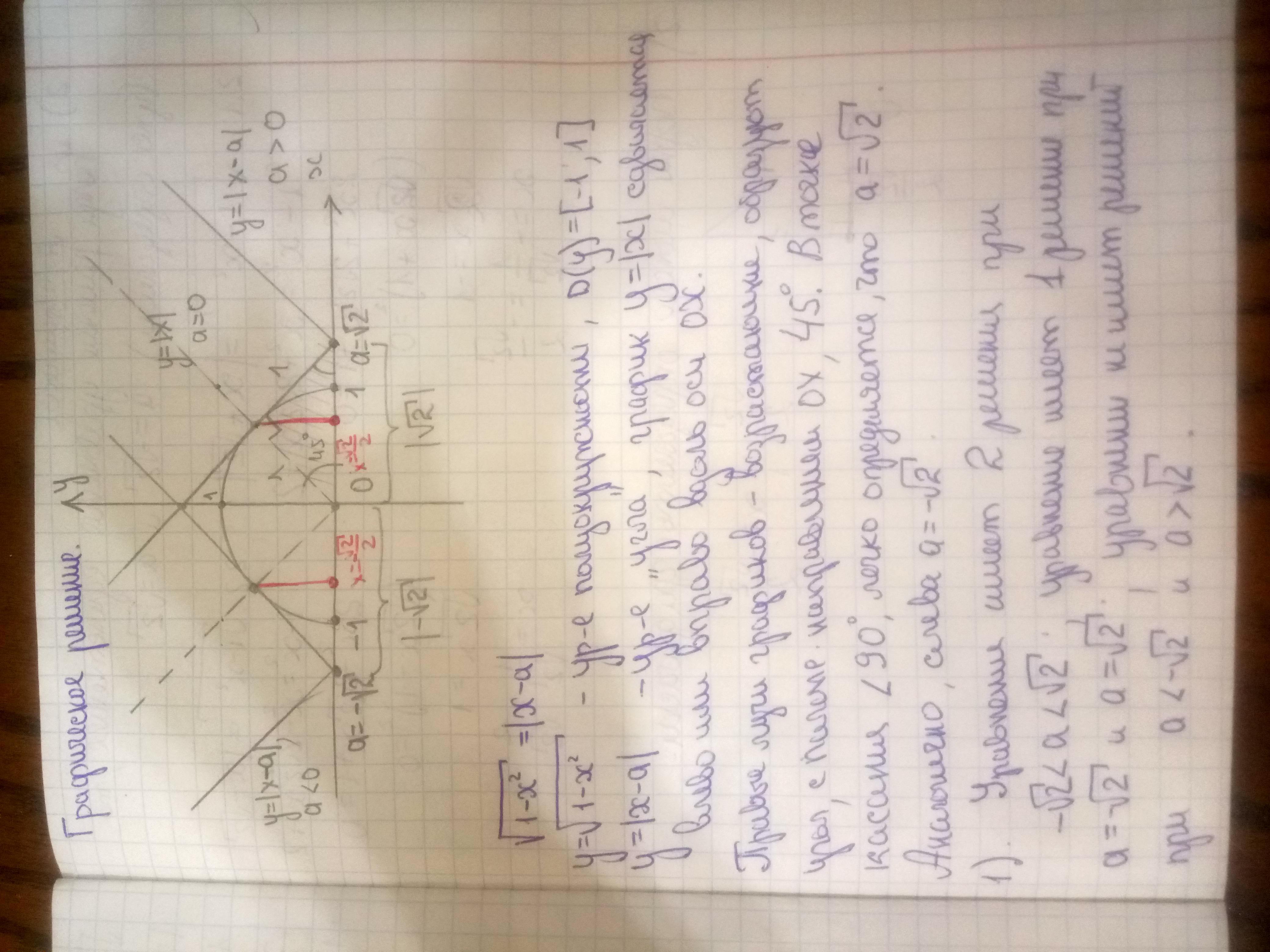
Эту задачу можно решать геометрически: левая часть уравнения задает верхнюю половину окружности, справа стоит "галка" модуля. Меняя значение параметра a, двигаем галку. Наша задача - добиться касания галки и полуокружности.

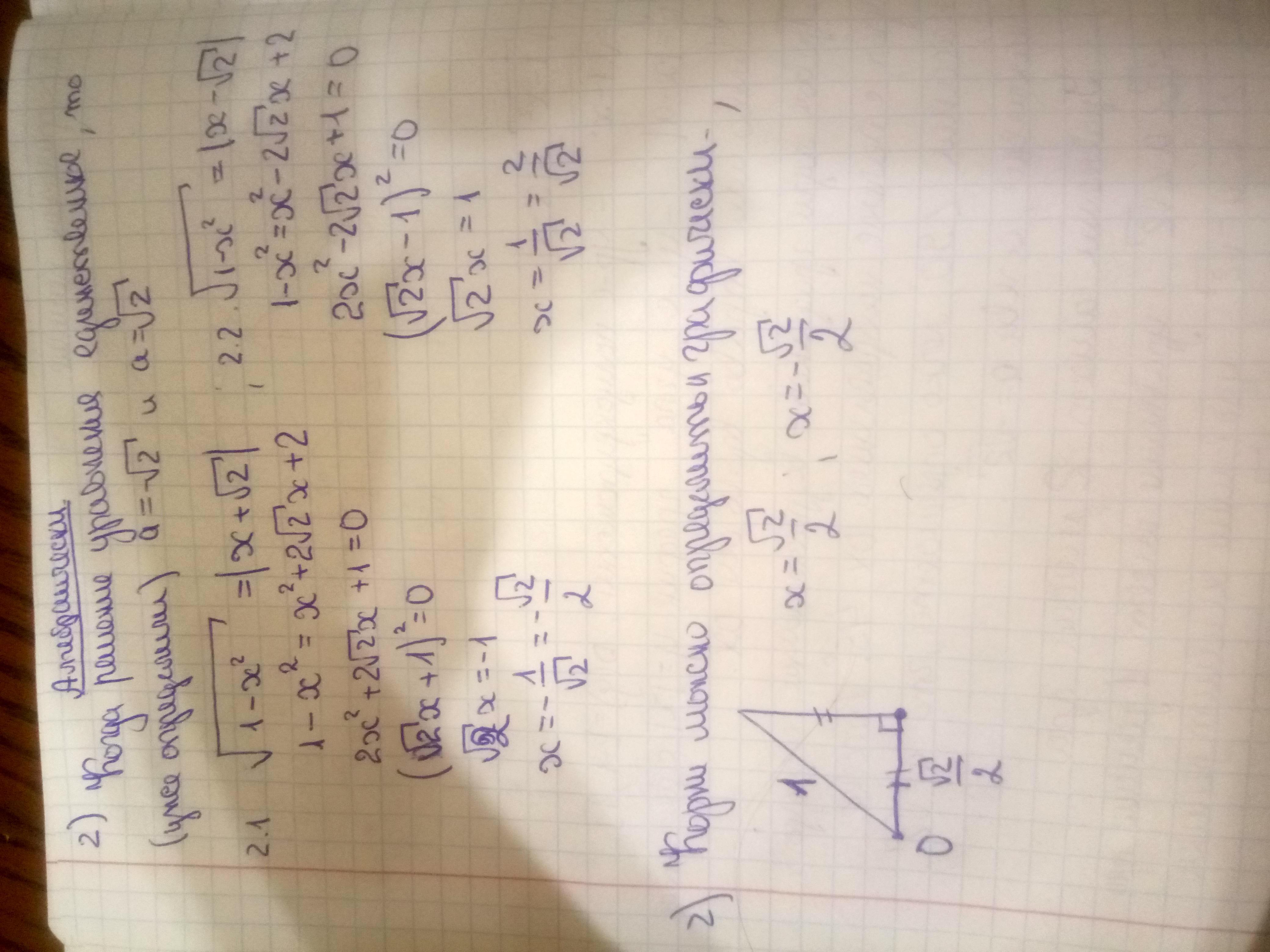
Но мы пойдем другим путем и решим задачу чисто алгебраически. Учитывая, что правая часть неотрицательна, возведение уравнения в квадрат приведет к равносильному уравнению:

$sqrt{1-x^2}=|x-a|Leftrightarrow 1-x^2=x^2-2ax+a^2; 2x^2-2ax+a^2-1=0.$

Квадратное уравнение имеет единственное решение тогда и только тогда, когда дискриминант равен нулю:

$D=4a^2-8a^2+8=0;a^2=2; a=pm sqrt{2}.$

Остается найти решение при найденных a:

$x=frac{2a}{4}=frac{a}{2}.$

Ответ: $a=sqrt{2}Rightarrow x=frac{sqrt{2}}{2}; a=-sqrt{2}Rightarrow x=-frac{sqrt{2}}{2}$

Answer 2

Решение задания приложено