Ответы
Ответ дал:
17
Координаты вектора=(х2-х1); (у2-у1)
ДА((5-2);(7-6))=(3;1)
СВ((6-3); (4-3))=(3;1) ⇒ векторы ДА и СВ параллельны и равны; т.к. векторы имеют одинаковые координаты.
АВСД - параллелограмм по признаку - противоположные стороны параллельны и равны.
IДАI=√(3²+1²)=√10; координаты вектора СД((2-3);(6-3))=(-1;3)
IСДI=√((-1)²+3²)=√10
Смежные стороны параллелограмма равны.
Параллелограмм с равными сторонами - ромб.
Диагонали ICAI и IВДI равны по √20=2√5, значит АВСД не просто ромб, а квадрат))
Приложения:
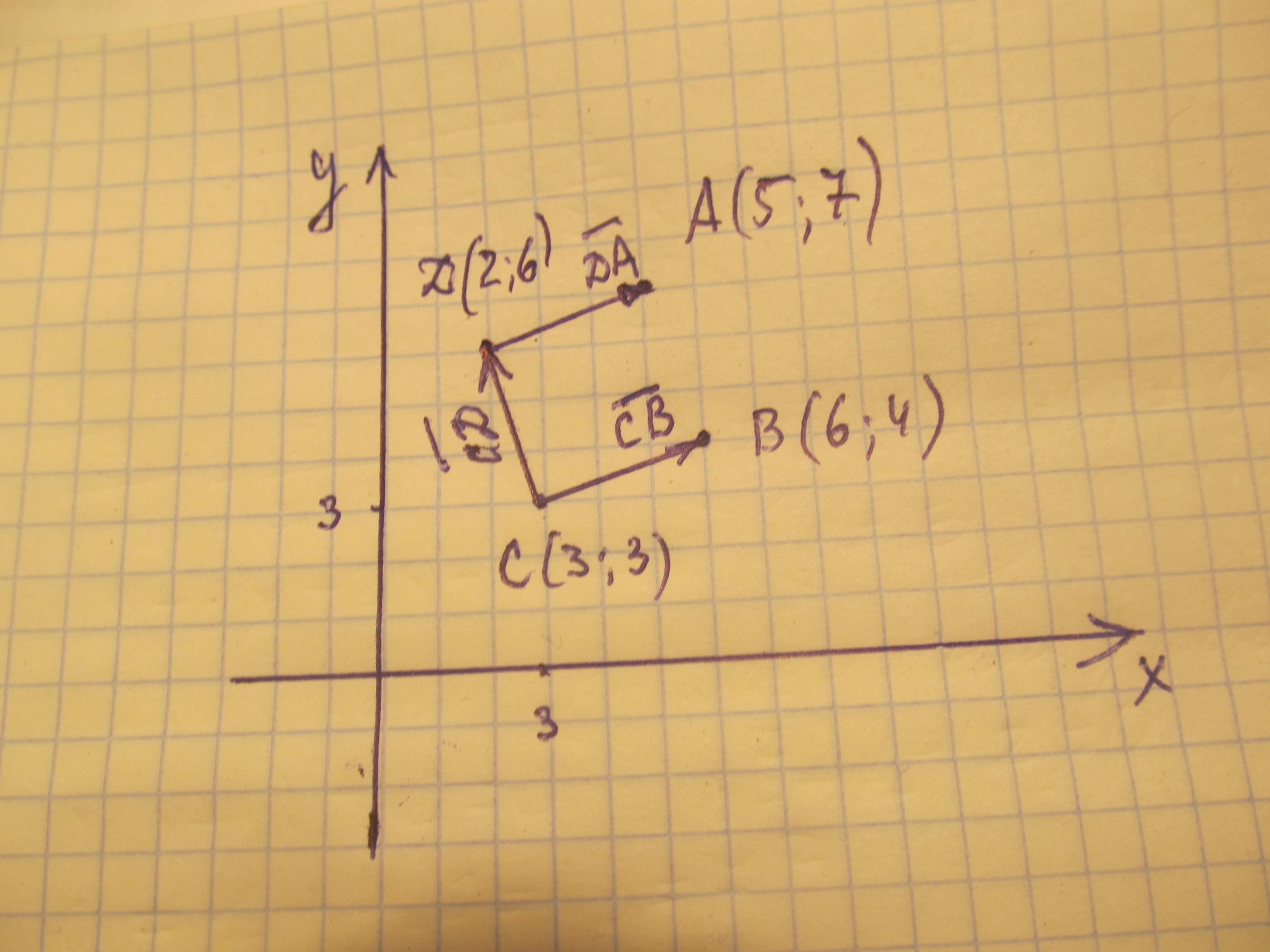
Вас заинтересует
1 год назад
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад